高一数学第一学期半期考试试卷
(完卷100分钟 满分100分)
班级____________座号__________成绩___________
一、选择题(每小题4分,共40分)(答案请做在答题纸上)
1.已知集合![]() ,
,![]() ,则集合
,则集合![]() ( )
( )
A .{0} B.{1,2} C.{1} D.{2}
2.若![]() ,则实数
,则实数![]() 的取值范围是
( )
的取值范围是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知函数![]() 在(1,2)有一个零点则实数
在(1,2)有一个零点则实数![]() 的值范围是 ( )
的值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]()
4.某电子公司七年来,生产VCD机总产量C(万台)与生产时间t(年)的函数关系如图,下列四种说法
|
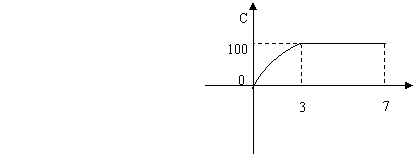
(1)前3年中,产量增长速度越来越快;
(2)前3年中,产量增长速度越来越慢;
(3)三年后,这种产品停止生产;
(4)三年后,年产量保持为100万台;
其中说法正确的是 ( )
A.(1)(3) B.(2)(3) C.(2)(4) D.(1)(4)
2. 已知 ![]() ,则
,则![]() =
( )
=
( )
A.![]() B.
B.![]() C.
C. ![]() D.
D.
![]()
6.函数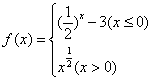 ,已知
,已知![]() ,则实数
,则实数![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
7.已知![]() ,
,![]() 若
若![]() 那么
那么![]() 与
与![]() 在同一坐标系内的图像可能是
( )
在同一坐标系内的图像可能是
( )
|
|

 8.二次函数
8.二次函数| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
则不等式![]() 的解集为
( )
的解集为
( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
9.设函数![]() 为奇函数,且
为奇函数,且![]() ,
,![]() ,则
,则![]() ( )
( )
A.0
B.1
C.![]() D.5
D.5
10.已知![]() 恒过定点(2,0),则
恒过定点(2,0),则![]() 的最小值为 ( )
的最小值为 ( )
A.5
B.![]() C.4
D.
C.4
D.![]()
二、填空题(每小题3分,共12分)(答案请做在答题纸上)
11. 。
。
12.已知函数![]() 有四个零点,则实数
有四个零点,则实数![]() 的取值范围是
的取值范围是![]() 。
。
13.若![]() 的定义域为[1,2],则
的定义域为[1,2],则![]() 定义域为
定义域为![]() 。
。
14.已知![]() 是定义在集合
是定义在集合![]() 上的偶函数,
上的偶函数,![]() 时
时![]() ,则
,则![]() 时
时![]() 。
。
福州一中2007—2008学年第一学期半期考试
高一数学答题纸
(完卷100分钟 满分100分)
班级____________座号__________成绩___________
一、选择题(每小题4分,共40分)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
二、填空题(每小题3分,共12分)
11.![]() ;
12.
;
12.![]() ;
;
13.![]() ;
14.
;
14.![]() 。
。
三、解答题(第15题8分,第16-19题每题10分,共48分)
15.已知集合![]() ,
,![]() ,
,![]() ,全集
,全集![]() 。
。
(1)若![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
(2)若![]() ,求
,求![]() 的取值范围。
的取值范围。
16.已知函数![]() ,
,
(1)当![]() 时,函数
时,函数![]() 恒有意义,求实数
恒有意义,求实数![]() 的取值范围。
的取值范围。
(2)是否存在这样的实数![]() ,使
,使![]() 在区间
在区间![]() 上为减函数,且最大值为1,若存在,求出
上为减函数,且最大值为1,若存在,求出![]() 的值,若不存在,说明理由。
的值,若不存在,说明理由。
17.已知![]() (1)若
(1)若![]() 为奇函数,求
为奇函数,求![]() 的值;(2)在(1)的条件下,求
的值;(2)在(1)的条件下,求![]() 的值域。
的值域。
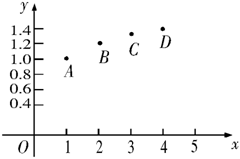
18.由于生态环境改善,某水库的鱼逐步增加,直到一个稳定生态平衡状态,经测算前4个月鱼的数量分别为1万尾,![]() 万尾,
万尾,![]() 万尾,
万尾,![]() 万尾,现给出两个函数模型:
万尾,现给出两个函数模型:
(1)![]() (2)
(2)![]()
其中![]() 表示月份,
表示月份,![]() 表示数量,你认为应该选择哪个模型最接近客观实际?并说明理由?
表示数量,你认为应该选择哪个模型最接近客观实际?并说明理由?
19.已知二次函数![]() 的二次项系数为
的二次项系数为![]() ,且不等式
,且不等式![]() 的解集是
的解集是![]() ,
,
(1)若![]() 有两个相等的根,求
有两个相等的根,求![]() 的解析式
的解析式
(2)若![]() 的最大值为正数,求
的最大值为正数,求![]() 的取值范围。
的取值范围。
高一数学试卷答案
(完卷100分钟 满分100分)
班级____________座号__________成绩___________
一、选择题(每小题4分,共40分)
CAABB BCBCB
二、填空题(每小题3分,共12分)
11.1; 12.![]() ; 13.[1,4]; 14.
; 13.[1,4]; 14.![]() 。
。
三、解答题(第15题8分,第16-19题每题10分,共48分)
15.已知集合![]() ,
,![]() ,
,![]() ,全集
,全集![]() 。
。
(1)若![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
(2)若![]() ,求
,求![]() 的取值范围。
的取值范围。
解:
(1)由于![]() ,于是
,于是![]()
(2)显然![]() ;
;
由于![]() ,于是
,于是![]()
![]() ,于是
,于是![]()
于是![]()
16.已知函数![]() ,
,
(1)当![]() 时,函数
时,函数![]() 恒有意义,求实数
恒有意义,求实数![]() 的取值范围。
的取值范围。
(2)是否存在这样的实数![]() ,使
,使![]() 在区间
在区间![]() 上为减函数,且最大值为1,若存在求出
上为减函数,且最大值为1,若存在求出![]() 的值,若不存在,说明理由。
的值,若不存在,说明理由。
解:![]() 由函数
由函数![]() 和函数
和函数![]() 复合而成
复合而成
(1) 由已知,对一切的![]() ,
,![]() 恒大于0,
恒大于0,
即函数![]()
![]() 的最小值大于零;
的最小值大于零;
又因为![]() 且
且![]() ,于是
,于是![]() 为减函数,
为减函数,
于是当![]() 时,
时,![]() ,即
,即![]()
综上可知,![]() 且
且![]() 。
。
(2) 假设存在满足题意的![]() ;
;
由于![]() 在区间
在区间![]() 上为减函数,
上为减函数,
于是在区间![]() 上,
上,![]() ,
,
于是![]() ;
;
又因为![]() 在区间
在区间![]() 上为减函数且函数
上为减函数且函数![]() 也为减函数, 于是函数
也为减函数, 于是函数![]() 为增函数,于是
为增函数,于是![]() ;
;
又因为![]() 在区间
在区间![]() 恒有意义,于是
恒有意义,于是![]() 且
且![]()
显然![]() 不满足上述条件。
不满足上述条件。
综上所述,不存在满足题意的![]() 。
。
17.已知![]()
(1)若![]() 为奇函数,求
为奇函数,求![]() 的值;
的值;
(2)在(1)的条件下,求![]() 的值域。
的值域。
解:
(1)
由于![]() 为奇函数,于是
为奇函数,于是![]() ,
,
即![]() ,解之得
,解之得![]() 。
。
(2)由(1)得![]() ,于是
,于是![]()
于是![]()
18.由于生态环境改善,某水库的鱼逐步增加,直到一个稳定生态平衡状态,经测算前4个月鱼的数量分别为1万尾,![]() 万尾,
万尾,![]() 万尾,
万尾,![]() 5万尾,现给出两个函数模型:
5万尾,现给出两个函数模型:
(1)![]() (2)
(2)![]()
其中![]() 表示月份,
表示月份,![]() 表示鱼的数量,你认为应该选择哪个模型最接近客观实际?并说明理由?
表示鱼的数量,你认为应该选择哪个模型最接近客观实际?并说明理由?

解:设月份数为x,第x月份鱼的数量为y万尾,建立平面直角坐标系,可得![]()
(1)构建二次函数模型
设![]() ,将
,将![]() 三点的坐标代入,
三点的坐标代入,
有![]() ,
,![]() ,
,![]() ,
,
解得 ![]() ,
,![]() ,
,![]() ,
,
故![]() .
.
将![]() 点的坐标代入,得
点的坐标代入,得
![]() ,与实际误差为0.025.
,与实际误差为0.025.
(2)构建指数函数模型
设![]() ,将
,将![]() 三点的坐标代入,有
三点的坐标代入,有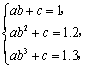 ,
,
解得 ![]() .
.
故![]() .
.
将![]() 点的坐标代入,得
点的坐标代入,得![]() ,与实际误差为0.025.
,与实际误差为0.025.
比较上述2个模拟函数的优劣,既要考虑到与实际误差最小,又要考虑到实际问题,比如鱼群最终要达到一个稳定生态平衡状态.经过筛选可以认为![]() 最佳,一是误差较小,二是由于生态环境改善,水库的鱼逐步增加,最终要达到一个稳定生态平衡状态,也就是说鱼群的数量最终要趋于稳定。而
最佳,一是误差较小,二是由于生态环境改善,水库的鱼逐步增加,最终要达到一个稳定生态平衡状态,也就是说鱼群的数量最终要趋于稳定。而![]() 恰好反映了这种趋势,因此选用
恰好反映了这种趋势,因此选用![]() 与实际生产比较接近.
与实际生产比较接近.
19.已知二次函数![]() 的二次项系数为
的二次项系数为![]() ,且不等式
,且不等式![]() 的解集是
的解集是![]() ,
,
(1)若![]() 有两个相等的根,求
有两个相等的根,求![]() 的解析式
的解析式
(2)若![]() 的最大值为正数,求
的最大值为正数,求![]() 的取值范围。
的取值范围。
解:
(1)因为![]()
所以![]()
于是![]() ①
①
由方程![]() ②
②
因为方程②有两个相等的根,所以![]() ,
,
即 ![]()
由于![]() 代入①得
代入①得![]() 的解析式
的解析式
![]()
(2)由![]()
及![]()
由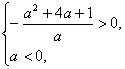 解得
解得 ![]()
故当![]() 的最大值为正数时,实数a的取值范围是
的最大值为正数时,实数a的取值范围是![]()