姓名_______ 高一数学第一学期数学期中测验试卷
__考室___________________号
班级______班 撰稿:方锦昌 电子邮箱 fangjingchang2 或@.com 手机:
一、选择题:(5×10=50′)
★1、已知全集![]() :
:
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
★2、下列指数式与对数式互化不正确的一组是:
A.
![]() B.
B.
![]()
C. ![]() D.
D. ![]()
★3、设![]() ,用二分法求方程
,用二分法求方程![]() 内近似解的过程中得
内近似解的过程中得![]() 则方程的根落在区间:
则方程的根落在区间:
A.(1,1.25) B.(1.25,1.5) C.(1.5,2) D.不能确定
 ★4、
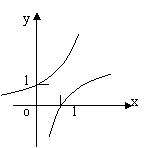
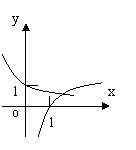
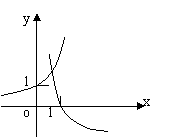
★4、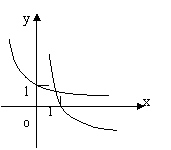 当
当![]() 时,在同一坐标系中,函数
时,在同一坐标系中,函数![]() 的图象是:
的图象是:
.
A B C D
★5、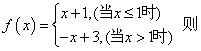
![]() :
:
A.3 B,2 C.1 D.0
★6、方程![]() 的实数解的个数是:
的实数解的个数是:
A.3 B.2 C.1 D.0
★7、如果二次函数![]() 有两个不同的零点,则m的取值范围是:
有两个不同的零点,则m的取值范围是:
A.(-2,6)
B.[-2,6]
C.(-2,6]
D.![]()
★8、某同学从家里到学校,为了不迟到,先跑,跑累了再走余下的路,设在途中花的时间为t,离开家里的路程为d,下面图形中,能反映该同学的行程的是:
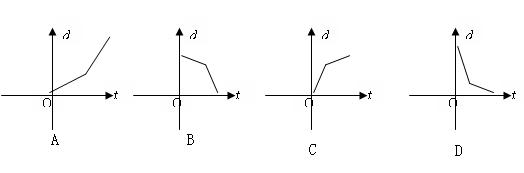
★9、设![]() 均为正数,且
均为正数,且![]() ,
,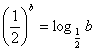 ,
,![]() .
. 则:
则:
A.![]() B.
B. ![]()
C. ![]() D.
D.
![]()
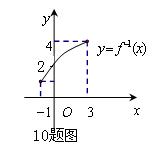
★10、函数![]() 的反函数
的反函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点
![]() (如10题图所示),则方程
(如10题图所示),则方程![]() 在
在![]() 上的根是
上的根是![]() :
:
A.4 B.3 C. 2 D.1
●选择题答案
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答 案 |
二、 填空题(5×5=25′)
★11、函数![]() 的定义域是_________________
的定义域是_________________
★12、若函数![]() 是偶函数,则
是偶函数,则![]() 的增区间是 _________
的增区间是 _________
★13、1992年底世界人口达到54.8亿,若人口的年平均增长率为x℅,2005年底世界人口为y(亿),那么y与x的函数关系式为 ;
★14、设函数![]() 在
在![]() 内有定义,下列函数:
内有定义,下列函数:![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
![]() 其中必为奇函数的有_______________(要求填写正确答案的序号)
其中必为奇函数的有_______________(要求填写正确答案的序号)
★15、国家规定个人稿费纳税办法为:不超过800元的不纳税;超过800元而不超过4000元的按超过部分的14%纳税;超过4000元的按全部稿酬的11%纳税.李宇春出名后出版了一本书共纳税420元,则她所获得的稿费为 __________元
三、 解答题(10+12+12+13+14+14=75′)
★16题(10分): 已知集合A=![]() -1,3,2
-1,3,2![]() -1
-1![]() ,集合B=
,集合B=![]() 3,
3,![]()
![]() .若B
.若B![]() A,求实数
A,求实数![]() 之值。
之值。
★17题:计算:(每小题6分,共12分)
(1)(1)![]() +
+![]()
(2)计算![]() -
- ![]()
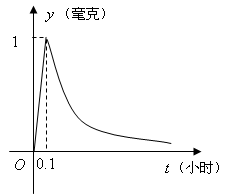 ★18题(12分)、为了预防流感,洞口三中决定于11月20日上午8点开始对教室用药熏消毒法进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为
★18题(12分)、为了预防流感,洞口三中决定于11月20日上午8点开始对教室用药熏消毒法进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为![]() (a为常数),如图所示,根据图中提供的信息,回答下列问题:
(a为常数),如图所示,根据图中提供的信息,回答下列问题:
(Ⅰ)从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式为多少?
(Ⅱ)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那么从药物释放开始,至少需要经过多少个小时后,学生才能回到教室.
★19题(13分)、设![]() ,函数
,函数![]() 有最大值,求不等式
有最大值,求不等式![]() 的解集。
的解集。
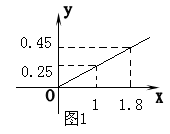
★20题(14分):洞口县三可食品有限公司生产冷冻肉(记为产品A)和柑桔罐头 (记为产品B)这两种产品,根据往年的市场调查以及对今年的市场进行预测,发现产品A的利润与其投资额成正比,其关系如图1所示;产品B的利润与其投资额的算术平方根成正比,其关系如图2所示(注:利润以及投资额的单位均为:万元).
(1)、分别将产品A、产品B的利润表示为投资额的函数关系式,并写出来;(3分+3分)
(2)、现在三可食品有限公司已筹集到了10万元投资,并计划全部抽入A、B两种产品的生产,问:应怎样分配这10万元提资,才能使三可食品有限公司所能获得的利润达到最大,所能达到的最大利润又约为多少万元?(精确到1万元).(8分)
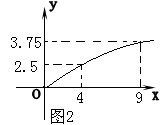
★
21题(14分):已知函数f(x)=![]() (其中a>0,且a≠1) ,
(其中a>0,且a≠1) ,
(1)、求出函数f(x)的定义域M;(3分) (2)、讨论f(x)的奇偶性;(3分)
(3)、若函数f(x)存在有:当x∈[m,n](且[m,n]ÜM )时,其值域恰好为[logan+1,logam+1];则请回答:(i)求证:0<a<1,且函数f(x)为↘;(ii)、求出在此条件下的a之取值范围。(3+5分)
参考答案(2007年11月18日)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | C | B | A | B | B | D | C | A | C |
第11题: x≥16; 第12题: ![]() 或者
或者![]() ; 第13题:
; 第13题: ![]() ;
;
第14题:(2),(4), 第15题: 3800元;
★16题:
解(10分):由![]() ,经检验,
,经检验,![]() 为所求;
为所求;
★17(12分): (1)、; (2)、![]() -4。
-4。
★18(12分)、(1)、解: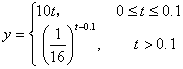 ;
(2)、
;
(2)、 ![]() 。
。
★19(12分)、
解: 设![]() ,函数
,函数![]() 有最大值,
有最大值,
∵![]() 有最小值,
有最小值,
∴ 0<a<1, 则不等式![]() 的解为
的解为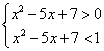 ,
,
解得2<x<3,所以不等式的解集为![]() .
.
★20题(14分):
解:(1)yA=x(x≥0), yB= (x≥0);
(2)设产品A投入x万元,则产品B投入(10-x)万元,则y= + (0≤x≤10),令=t,则y= (t-)2+ (0≤t≤),则当t=,即当x=10-=3.75时,ymax=≈4,故产品A投资额为3.75万元,产品B投资额为6.25万元时,三可公司有最大利润约为4万元.
★21题(14分):
解:(1)、M={xx<-2或x>2}; (2)、奇函数; (3)、0<a<