高一数学上学期期末考试卷
（必修Ⅱ）
命题人：
(时间：120分钟 满分：100分)
一、选择题：（3×14＝42分）
1、若a、b是异面直线，直线c∥a，则b与c的关系（ ）
A．平行 B．异面 C．不相交 D．不平行
2、一个直立在水平面上的圆柱体的正视图、俯视图、侧视图分别是（ ）
A．矩形、矩形、圆 B．矩形、圆、矩形
C．圆、矩形、矩形 D．圆、矩形、圆
3、若三个平面两两相交，有三条交线，则下面命题正确的是（ ）
A．三条交线两两异面 B．三条交线两两平行
C．三条交线交于一点 D．三条交线两两平行或交于一点
4、直线3x＋
y＋1＝0的倾斜角是（ ）
A．30° B．60° C．120° D．135°
5、如果AB>0，BC>0，那么直线Ax－By－C＝0不经过的象限是（ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
6、设圆O1的方程为(x－5)2＋(y－3)2＝9，圆O2的方程为x2＋y2－4x＋2y－9＝0，
则两圆的位置关系是（ ）
A．相交 B．内含 C．相离 D．相切
7、若直线ax＋by＝1与圆x2＋y2＝1有两个公共点，则点P(a，b)与圆的位置关系是（ ）
A．在圆上 B．在圆外 C．在圆内 D．以上皆有可能
8、方程x2＋y2＋2ax－2ay＝0(a≠0)表示的圆关于（ ）
A．x轴对称 B．y轴对称
C．直线y＝x对称 D．直线y＝－x对称
9、若三直线2x＋3y＋8＝0，x－y－1＝0和x＋ky＝0相交于一点，则k＝( )
A．－
B． C．－2 D．2
10、一棱台两底面周长的比为1∶5，过侧棱的中点作平行于底面的截面，则该棱台被分成两部分的体积比是（ ）
A．1∶125 B．27∶125 C．13∶62 D．13∶49
11、一个边长为a的正三角形，绕它的一条边所在直线旋转一周，所得几何体的体积为（ ）
A．
B．
C．
D．
12、长方体的表面积为11，十二条棱长度和为24，则长方体的外接球的直径为（ ）
A．2 B．
C．5 D．6
13、已知直线a、b和平面
，有以下四个命题：
①若a∥，a∥b，则b∥
②若
，
=B，则a与b异面
③若
，
，则
∥
④若a∥b，
，则，其中正确命题的个数是（
）
A．0 B．1 C．2 D．3
14、已知两点A(－1，2)，B(2，1)，直线l: 3x－my－m=0与线段AB相交，则直线l的斜率的取值范围是（ ）
A．
B．
C．[－3，1] D．
二、填空题：（共3＋5=8分）
15、直线x－y－2＝0关于点(1，2)对称的直线的方程是 .
16、⑴已知直线l与直线2x－3y＋1＝0垂直，且经过两直线6x－2y＋3＝0和3x＋y－2＝0的交点，试按以下步骤求l的方程:
①设l的方程为(6x－2y＋3)＋
(3x＋y－2)＝0;
②求得值为
；
③l的一般式方程为 .
⑵试类比⑴的解法，求经过圆x2＋y2－2x－2y－4＝0与直线2x－y－4＝0交点(不求交点)，且圆心在直线3x－2y＋7＝0上的圆的方程：
①设所求圆方程为 ；
②所求圆的圆心坐标用表示是
；
③圆的一般方程是 .
三、解答题：（共50分）
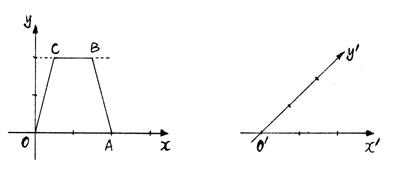
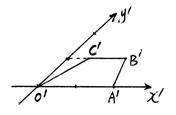
17、(4分)如图，OABC是水平放置的等腰梯形，其上底长是下底长的一半，试用斜二测画法画出它的直观图(不写作法，保留作图痕迹。)
18、(6分)求经过点(－3，4)，并且在两坐标轴上截距之和为12的直线的一般式方程。
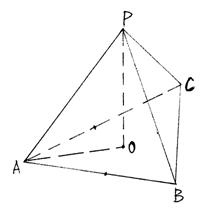
19、(8分)在三棱锥P－ABC中，PO
平面ABC，O为垂足，AO平分
.
⑴求证：
；
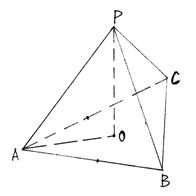⑵若
，
，PA=2，求PA与底面ABC所成角的大小，及二面角P－AB－C的正切值。
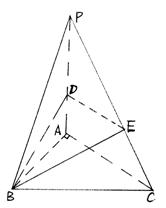
20、(10分)在三棱锥P－ABC中，PA平面ABC，，D、E分别是PA、PC边上的动点，且
(0<m<1).
⑴求证：AC∥平面BDE；
⑵求证：不论m为区间(0，1)内何值，总有平面BDE平面PAB；
⑶已知AB=AC=PA，是否存在m，使平面BDE平面PAC？若存在，求出m值；若不存在，说明理由.
 |
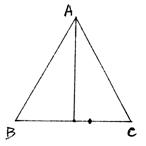
21、(8分)如图，等腰三角形ABC的底边BC长为2a(a>0)，BC边上的高为b(b>0)，试用解析法证明：底边上任一点(不含B、C)到两腰的距离之和等于一腰上的高.
 |
22、(14分)已知动点M分别到两个定点A、B的距离的比为正常数，求动点M 的轨迹方程.(要求：适当分类，通过几个实例(即A、B坐标和值均为具体数值)，分别求出M点轨迹方程，并依此猜想M点轨迹的位置特点. 若是圆，请化为标准方程.)
莆田一中2006～2007学年上学期期末考答题卷
高一数学(必修Ⅱ)
一、选择题：（3×14＝42分）请填在答题卡中
二、填空题：（共3＋5=8分）
15、 .
16、⑴② ；③ .
⑵① ；② ；③ .
三、解答题：（共50分）
17、(4分)
18、(6分)
19、(8分)
20、(10分)
21、(8分)
22、(14分)
23、(附加题：10分，计入总分，但不超过100分)
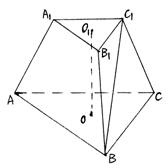
如图，三棱台ABC－A1B1C1的两底面均为正三角形，O1、O分别为两底面中心，且O1O底面，下底边长为4，上底边长为2，高O1O为2. 当三棱台绕直线OO1旋转一周时，由侧面BB1C1C的对角线BC1旋转产生的曲面记为W，试画出W的草图（直观图），并指出所画图形中的主要数据.
 |
上学期期末考参考答案
高一数学（必修Ⅱ）
一、选择题：（3×14＝42分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 答案 | D | B | D | C | B | A | B | D | A | D | B | C | B | D |
二、填空题：共3＋5=8分
15、x－y＋4＝0 16、⑴－6，12x＋8y－15＝0
⑵x2＋y2－2x－2y－4＋(2x－y－4)＝0， (1－,1＋
)，
x2＋y2＋2x－4y－12＝0
三、解答题：共50分
17、(4分)
 |
（注：有严重错误的不给分；看上去有误差的扣1分）
18、(6分)解：设所求直线的方程为
将(－3，4)代入，得－3b＋4a＝ab ①
又有a＋b＝12 ② （2分）
联立①②得a2－5a－36＝0→a＝－4或9 （4分）
所求直线方程是4x－y＋16＝0或x＋3y－9＝0 （6分）
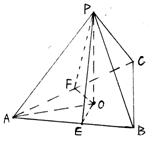
19、(8分)⑴证明：过O作OEAB于E，OFAC于F，
连结PE，PF （1分）
又∵
，AO＝AO
∴
（2分）
∴AE＝AF，OE＝OF
∵PO面ABC ∴POOE，POOF
∴
，得PE＝PF
从而
，∴
即 （4分）
⑵解：∵PO面ABC，∴
为PA与底面所成的角
∵POAB，OEAB，∴AB面POE，∴ABPE
为二面角P－AB－C的平面角 （6分）
在
中，AE＝PA·
，在
中，
∴在
中，
，
∵
，OE＝1，∴
，
（答略） （8分）
20、(10分)证明
：⑴∵
，∴AC∥DE
又∵AC
面BDE，DE
面BDE，∴AC∥面BDE （3分）
⑵∵PA面ABC，∴PAAC，又∵ABAC，∴AC面PAB
由⑴知，不论m为(0，1)内何值(任意
(0，1))，都有DE∥AC，
∴DE面PAB，又∵DE面BDE
∴对任意(0，1)，总有平面BDE平面PAB （6分）
（注：没有“不论m”或“任意m”说法的应扣1分。）
⑶不存在(0，1)，使平面BDE平面PAC （7分）
假设平面BDE平面PAC，∵面BDE
面PAC=DE，DEBD
∴BD面PAC，从而BDPA
在
中，D与A不重合，∴BD不垂直于PA，产生矛盾！
∴假设不正确，证得平面BDE与平面PAC不可能垂直。 （10分）
21、(8分)解：以BC中点O为原点，BC边上的高所在
直线为y轴建立直角坐标系， （1分）
则B(－a，0)，C(a，0)，A(0，b)，
设BC上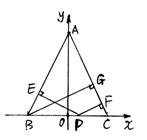
任一点P(x，0)(－a<x<a) （2分）
∵AB方程为
，即bx－ay＋ab＝0
AC方程为
，即bx＋ay－ab＝0（4分）
P到AB的距离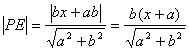
P到AC的距离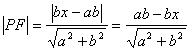
∴
，又B到AC的距离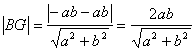
∴
，命题得证。
22、(14分)解：（应该对值进行分类，而不是对A、B进行分类。）
设A(－1，0)，B(1，0)，M(x，y)
⑴当=1时，
，M点轨迹是线段AB的中垂线，方程为x=0。
⑵当=时，
， 即
平方得3x2＋3y2＋10x＋3＝0，∴M点轨迹方程是
⑶当＝2时，
，即
平方得3x2＋3y2－10x＋3＝0，∴M点轨迹方程是
（6分）
轨迹特点：
①＝1时轨迹为直线，其余均为圆；
②≠1时，圆心C与A、B共线；
③当0<<1时，圆心偏向A一侧；当>1时，圆心偏向B一侧；
④当1•2＝1时，两圆关于线段AB的中点（或说中垂线）对称。（14分）
23、（10分）
画图要求：两底均为椭圆形，上底窄，下底宽，
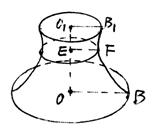缩腰，侧面为曲面。 （5分）
其中，
，
，
，
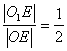（10分）
（注：附加题仅两种给分标准。）