高一数学上学期期末考试试题
高一数学试题
(总分:150分 考试时间:120分钟)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个备选项中,只有一项是符合题目要求的.
1. 对数![]() 互为相反数,则有( )
互为相反数,则有( )
A.![]() B.
B.![]() C.ab = 1 D.
C.ab = 1 D.![]()
2. 数列1,3,6,10,15……的一个通项公式为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3. 设命题![]() ,命题
,命题![]() ,则
,则![]() 的( )
的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
4. 对于定义在R上的任何奇函数![]() ,均有( )
,均有( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5. 等比数列{an}中,S3∶S2 = 3∶2,则公比q的值为( )
A.1 B.![]() C.
C.![]() D.
D.![]()
6. 等差数列![]() 等于( )
等于( )
A.13 B.26 C.52 D.156
7. 函数![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8. 函数![]() 在同一直角坐标系中的图像可能是( )
在同一直角坐标系中的图像可能是( )
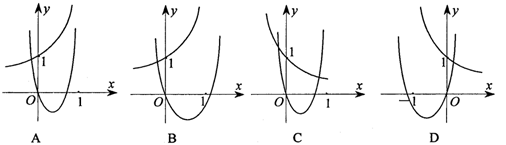
9. 数列{an}中,![]() ,数列{an}的前n项和Sn,那么S2005=( )
,数列{an}的前n项和Sn,那么S2005=( )
A.1002 B.1002.5 C.1003 D.1003.5
10. 设函数![]() 的大小关系是( )
的大小关系是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题:本大题共6小题,每小题4分,共24分.把答案填写在答题卡相应位置上.
11. 函数![]() 的定义域是______________.
的定义域是______________.
12. 已知数列{an}的前n项和为Sn,![]() ,则an =
.
,则an =
.
13. 某地区现有绿地1000亩,计划以后三年每年比前一年增加10%,则三年后绿地的亩数是_____________.
14. 若数列![]() 的值是
.
的值是
.
15. 函数![]()
![]() 则函数
则函数![]() 的递减区间是
.
的递减区间是
.
16.设等差数列:![]() 的值是
的值是
三、解答题:本大题共6小题,共76分,解答应写出文字说明、证明过程或演算步骤.
17.(10分) 求值:![]() .
.
18.(14分) 已知![]() 是等差数列,其前
是等差数列,其前![]() .
.
(1)
求数列![]() 的通项公式;
的通项公式;
(2)
设![]() ,证明
,证明![]() 是等比数列,并求数列
是等比数列,并求数列![]() 的前
的前![]() 项和
项和![]() .
.
19.(14分) 已知![]() ,求函数
,求函数![]() 的最大值和最小值.
的最大值和最小值.
20.(13分) 已知函数![]() .
.
(3)
求![]() 的表达式,写出其定义域,并判断奇偶性;
的表达式,写出其定义域,并判断奇偶性;
(4)
求![]() 的表达式,并指出其定义域;
的表达式,并指出其定义域;
(5)
判断![]() 单调性并证明.
单调性并证明.
21.(12分) 已知二次函数![]() 同时满足以下条件:
同时满足以下条件:
①![]() ,②
,②![]() ,③对任意实数
,③对任意实数![]() 恒成立.
恒成立.
(6)
求![]() 的表达式;
的表达式;
(7)
若![]() 为等比数列,
为等比数列,![]() 的最大值;
的最大值;
(8)
令![]() 试求
试求![]() 的最大值.
的最大值.
22.(13分) 已知等比数列![]() ,
,
(9)
求![]()
![]() 的通项公式;
的通项公式;
(10)设![]() .
.
(命题人:周 静 审题人:赵胜敏)
重庆市西南师大附中2007—2008学年度上学期期末考试
高一数学试题参考答案
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个备选项中,只有一项是符合题目要求的.
1.C 2.A 3.A 4.A 5.C 6.B 7.C 8.A 9.B 10.C
二、填空题:本大题共6小题,每小题4分,共24分.
11.![]() 12.6 n – 5
12.6 n – 5![]() 13.1331
13.1331
14.9902 15. ![]() 16.
16.![]()
三、解答题:本大题共6小题,共76分.
17.解:原式![]()
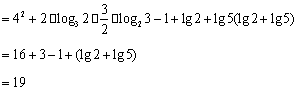
18.解:(1) 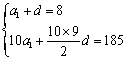
解得:d = 3,a1 = 5,∴
![]()
(2) ![]() ∴
∴ ![]()
∴ {bn}是公比为8的等比数列
∵ ![]()
∴ ![]()
19.解:由![]()
令![]()
![]()
∴ 当![]()
当![]()
20.解:(1) 当![]()
由a1 = 3得:S1 = a1 = 2a + b = 3
又{an}等比数列,∴ a1 = a = 3
于是![]() ∴ 通项公式
∴ 通项公式![]()
(2) ![]() ∴
∴ ![]() ①
①
![]() ②
②
①-②得: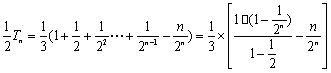
∴![]()
21.解:(1) 令![]() ,∴
,∴ ![]() ,
,
∴ ![]()
∴ ![]() 其定义域为(– 1,1),其定义域关于原点对称
其定义域为(– 1,1),其定义域关于原点对称
![]()
∴ ![]() 为奇函数
为奇函数
(2) 由![]()
∴ ![]()
由于![]()
![]() ,
,
∴ ![]() 即原函数值域R.
即原函数值域R.
∴ ![]() 的定义域为R
的定义域为R
(3) 设x1
< x2,则![]()
1°,a > 1时,![]() ,此时,
,此时,![]() ,函数
,函数![]() 单增
单增
2°,0 < a < 1时,![]() ,此时,
,此时,![]() ,函数
,函数![]() 单减
单减
22.解:(1) 由条件得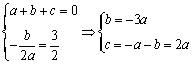
由![]() 恒成立
恒成立
∴ 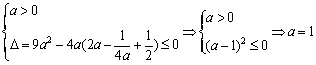
∴ ![]()
∴ ![]()
(2) 由(1)知![]()
![]()
![]()
![]()
而函数![]() 为减函数,知:
为减函数,知:![]()
即数列{Sn}的最大项为第一项
(3) ![]()
∴ ![]()
∴ ![]()
而![]()
∵ ![]() ,
,
![]()
故数列{Tn}中的最大项为第8项.