高一数学上学期阶段考试卷

高一数学上学期阶段考试卷

高一  数学(必修1)

 命题人：

(时间：120分钟　 满分：100＋8分)

一、选择题：（8×3=24分）

1、以下几位数学家对方程求解都做出了贡献，其中的中国数学家是（　）

　　A．贾宪　　　　　　B．费拉里　　　　　C．阿贝尔　　　　 D．伽罗瓦

2、下列关于集合的说法中，正确的是（　）

A．绝对值很小的数的全体形成一个集合

B．方程x(x－1)²＝0的解集是{1，0，1}

C．集合{1，a，b，c}和集合{a，b，c，1}相等

D．空集是任何集合的真子集

3、下列各组函数中，表示同一函数的是（　）

A．y＝1，　　　　　　　　　　　　　　　　 B．y＝lgx²，y＝2lgx

C．y＝x，　　　　　　　　　　　　　　 D．，

4、下列函数中，在其定义域内既是奇函数又是减函数的是（　）

A．y＝－x³，　　　　　　　　　　　B．，

C．y＝x，　　　　　　　　　　　　　　　　　D．，

5、化简lg5·lg20＋lg²2的结果是（　）

　　A．2　　　　　　　　　B．1　　　　　　　　　　C．2lg2　　　　　　　 D．lg2·lg5

6、已知函数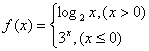，则的值是（  ）

　  A．　　　　　　　　 B．9　　　　　　　　　　C．－　　　　　　　D．－9

7、设集合A＝，B＝，若AB，则a的取值范围是（  ）

　　A．a1　　　　　　　　　　B．a<1　　　　　　　　C．a>2　　　　　　　 D．a2

8、若函数f(x)＝ax＋b(a0)有一个零点是－2，则函数g(x)＝bx²－ax的零点是（　）

　  A．2，0　　　　　　　　　 B．2，　　　　 C．0，　　　　D．0，

二、填空题：（6×3＋5＋6=29分）

9、已知集合A＝{1，a²}，实数a不能取的值的集合是　　　　　　  .

10、函数f(x)＝的定义域是　　　　　　　  .

11、函数y＝log₂(－x²＋2x＋7)的值域是　　　　　  .

12、已知函数y＝(k²＋k)·x^k为幂函数，则k的取值是　　　　 .

13、如右图所示，M、A、B是全集U的

三个子集，则图中阴影部分所显示的

集合可以表示为　　　　　　　　 .

14、已知函数f(x)满足：(1)对任意x₁<x₂，总有f(x₁)<f(x₂)；(2)对x₁、x₂R，都有f(x₁·x₂)＝f(x₁)·f(x₂)；(3)函数f(x)的图象不是直线。写出一个同时满足上述三个条件的函数解析式　　　　　　  .

15、在向空杯中匀速注水时，考虑杯中水面的高度h随时间t变化的函数h=f(t)(注满为止)：

　　⑴若给的是圆柱型无盖水杯(杯内深度为a)，请画出h＝f(t)的图象；

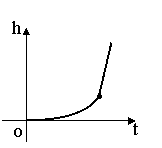
⑵若给出的是h＝f(t)的图象(右图)，请设计一个合适

的杯子(画出杯子的轮廓即可)。

16、已知全集U＝{}，集合A＝{}，B＝{}，

　　求：⑴ AB　　　　　 ⑵ AB　　　　　　 ⑶ (AB)　　　　　　 ⑷ (A)(B)

答：⑴　　　　　  ，⑵　　　　　 ，⑶　　　　　  ，⑷　　　　　　.

三、解答题：（6＋6＋7＋10＋8＋10=47分）

17、(6分)已知集合A＝{}，B＝{}，

且AB＝A，，，求实数a的值。

18、(6分)以下是用二分法求方程x³＋3x－5＝0的一个近似解(精确度为0.1)的不完整的过程，请补充完整(详见答案卷)。

19、(7分)已知某商品进价为每个40元，若按每个60元售出，能卖出150个。 经测算，若该商品零售价每增加1元，销售量将减少5个(设定按实际销量进货) 。 当零售价定为多少时，可赚得最大利润？最大利润是多少？

20、(10分)我市某企业常年产生一种出口产品，根据需求预测：进入21世纪以来，前8年在正常情况下，该产品产量将平稳增长. 已知2000年为第一年，头4年年产量f(x)(万件)如下表所示：

x	1	2	3	4
f(x)	4.00	5.58	7.00	8.44

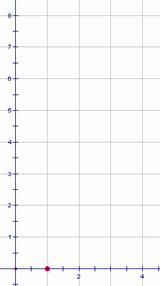
　  ⑴画出2000～2003年该企业年产量的散点图；

⑵建立一个能基本反映（误差小于0.1）这一时期该企业年产量发展变化的函数模型，并求之。

⑶2006年(即x＝7)因受到某外国对我国该产品反倾销的影响，年产量应减少30%，试根据所建立的函数模型，确定2006年的年产量应该约为多少？

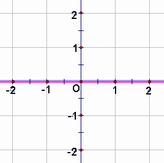
21、(8分)已知函数，试利用基本初等函数的图象，判断f(x)有几个零点；并利用零点存在性法则确定各零点所在的范围(各区间长度不超过1) 。

22、(10分)已知函数是奇函数，且

　  ⑴求函数f(x)的解析式；

⑵判断f(x)在(0，1)上的单调性，并用单调性定义证明。

23、附加题：（8分，计入总分）

　　问题：已知集合A＝{a，b，c}，B＝{m，n}，则从A到B的所有不同的映射的个数是　　　　  (此问不加分) 。请认真阅读以下内容：

例1：从甲地到乙地，可以乘火车，也可以乘汽车。 一天中，火车有3班，

汽车有2班。问：一天中乘火车或汽车从甲地到乙地共有几种不同的走法？

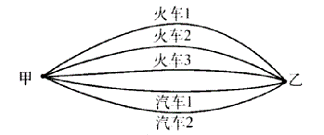
因为乘火车或乘汽车都可以完成“从甲地到乙地”这件事，所以共有3＋2=5种不同的走法。这符合“分类计数原理”（加法原理）：完成一件事，有几类办法，在第1类办法中有m₁种不同的方法，在第2类办法中有m₂种不同的方法……在第n类办法中有m_n种方法，那么完成这件事共有N＝m₁＋m₂＋…＋m_n种不同的方法。

例2：从甲地到乙地，要上午先从甲地乘火车到丙地，再于下午从丙地乘汽车到乙地。一天中，可乘的火车只有上午3班， 汽车下午只有2班。问：一天中这样从甲地到乙地共有多少种不同的走法？

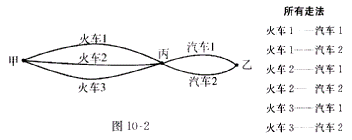
因为必须经过先乘火车、后乘汽车两个步骤，才能完成“从甲地到乙地”这件事，所以共有3×2＝6种不同的走法。这符合“分步计数原理”(乘法原理)：完成一件事，需要分成几个步骤，做第1步有m₁种不同的方法，做第2步有m₂种不同的方法……做第n步有m_n种不同的方法，那么完成这件事共有N＝m₁·m₂·…·m_n种不同的方法。

我们把本题开头的问题中“构成一个映射”看成“一件事”，请你选择上面的原理，对问题的结论加以说明。

莆田一中2006～2007学年上学期阶段考答案卷

高一数学(必修1)

一、选择题：（8×3=24分）请填在答题卡中

二、填空题：（6×3＋5＋6=29分）

9、　　　　  　10、　　　　　　  11、　　　　　　 　12、　　　　　　

13、　　　　 　　　　　　　　　　14、　　　　　　　　

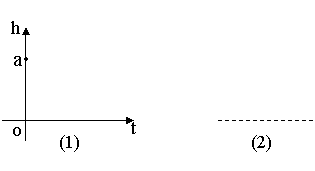15、(画图要用三角板)⑴　　　　　　　　　　　　　　　　　　　　　　　　　　　　⑵

　　　　　　　　　　　

16、⑴　　　　 ，⑵　　　　 ，⑶　　　　　　　　　 ，⑷　　　　　　　　 .

三、解答题：（6＋6＋7＋10＋8＋10=47分）

17、(6分)

18、(6分)解：设函数f(x)=x³＋3x－5，其图象在(－，＋)上是连续不断的。

先求值：f(0)＝　　　　 ，f(1)＝　　　　 , f(2)＝　　　　  , f(3)＝　　　　。

所以f(x)在区间　 　　　 内存在零点x₀，填表：

区  间	中点m	f(m)符号	区间长度

　　下结论：　　　　　　　　　　　　　　　　　　　　　　　　　　　　 .

(可参考条件：f(x)在(－，＋)上是增函数，且f(1.125)<0，f(1.1875)>0。

19、(7分)

20、（10分）

21、（8分）

22、（10分）

23、附加题：（8分）

莆田一中2006～2007学年上学期阶段考参考答案

高一数学(必修1)

一、选择题：（8×3=24分）A C C A B A B D

二、填空题：（6×3＋5＋6=29分）

9、{－1，1}　10、　11、　12、　13、(A)[A(M)]　　　

14、y＝x³(x)　　　　  16、⑴，⑵，⑶和⑷为(1，3)[5，7]

15、⑴　 · 　　⑵

　　　·　　　　　　　　　 (说明：15、⑴2分，⑵3分；16、错一空扣2分)

三、解答题：（47分）

17、(6分)解：由已知，A＝{－6，0}，BA，B　　　　　　　　　　　（1分）

　　　　　　 ∴B＝{－6}或{ 0 }　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（1分）

⑴若B＝{－6}，则

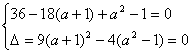
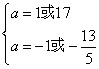   　∴ a无解　　　 （2分）

⑵若B＝{ 0 }，则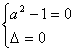　∴ a＝－1，故所求a的值是－1。（2分）

18、(6分) f(0)＝－5，f(1)＝－1，f(2)＝9，f(3)＝31(可以不求)

　　　　 ∴初始区间为(1，2)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （2分）

区　间	中点m	f(m)符号	区间长度
(1，2)	1.5	＋	1
(1，1.5)	1.25	＋	0.5
(1，1.25)	1.125	－	0.25
(1.125，1.25)	1.1875	＋	(3分)   0.125
(1.125，1.1875)			0.0625

　　∵，∴（不唯一）。　　　　　　 （1分）

19、(7分)解：设零售价增加x元时，可赚得最大利润，则能售出(150－5x)个，每个商品利润为60＋x－40＝x＋20（元）。

　  利润y＝(x＋20)(150－5x)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （3分）

　　　　 ＝－5x²＋50x＋3000

　　　 ＝－5(x－5)²＋3125　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　  ∵0x<30，∴当x＝5时，　　　　　　　　　　　　　　　　　　　　　　 （3分）

　  答：零售价为65元时，可得最大利润3125元　　　　　　　　　　　　　　　 （1分）

20、(10分)解：⑴如图(2分)，⑵设f(x)＝ax＋b　 （1分）

　　由已知得，解得，

　　∴　　　　　　　　　　　　　　　　　　　　　(2分)

　　检验：f(2)＝5.5，；

　　　　  f(4)＝8.5，

　　∴模型能基本反映产量变化。（2分）

⑶f(7)＝13，13×70%＝9.1，2006年产量应约为9.1万件。　　　　 （3分）

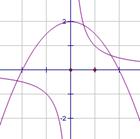21、(8分)解：由f(x)＝0，得

令,,其中抛物线顶点

为(0，2)，与x轴交于点(－2，0)、(2，0)（2分）

　  如图所示，y₁与y₂图象有3个交点，从而函数f(x)

有3个零点。　　　　　　　　　　　　　　　　　　　　　　 　（2分）

由f(x)知x0，f(x)图象在(－,0)、(0，＋)上分别是连续不断的，

且，，,,,

即f(－3)·f(－2)<0，·f(1)<0，f(1)·f(2)<0，　　　　　　　　　　　　　　　　（3分）

∴三个零点分别在区间(－3,－2)、(，1)、(1，2)内。　　　　　　　　　　　　 （1分）

22、(10分)解：⑴∵f(x)是奇函数，∴对定义域内的任意x，都有f(－x)＝－f(x),

　　即　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （2分）

　  整理得s－3x＝－s－3x，∴s＝0　　　　　　　　　　　　　　　　　　　　　　　　　　　　（1分）

　　由f(2)＝，得，∴r＝2

　　∴所求解析式为。　　　　　　　　　　　　　　　　　　　　　（2分）

　　(另解：若s0，则，定义域不关于原点对称，不合。

　　 ∴s＝0，这时f(x)＝, 不难验证f(x)为奇函数。下略。)

⑵f(x)＝－在(0，1)上为增函数，证明如下：　　　　　　　　　　（1分）

  设0<x₁<x₂<1　

  则f(x₁)－f(x₂)＝

　　　　　　 ＝

　　　　　　 ＝　　　　　　　　　　　　　　　　　　　　　　　 （2分）

　∵x₂－x₁>0，x₁·x₂>0，x₁x₂<1

　∴f(x₁)－f(x₂)<0，即f(x₁)<f(x₂)

　故f(x)在(0，1)上是增函数。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（2分）

23、附加题（8分）

答：构成一个映射可分成3个步骤进行：

第一步确定a的象有2种方法(m或n)；第2步确定b 的象有2种方法；第3步确定c的象有2种方法，则根据分步计数原理，完成“构成一个映射”的不同方法有N＝2×2×2＝8种，即不同映射的个数为8。