高一数学上期期末测试试题
数 学 2008.1
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至8页,共150分,考试时间120分钟。
第Ⅰ卷(选择题,共60分)
1.答第Ⅰ卷前,请务必将自己的姓名、准考证号、考试科目,用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在考题卷上。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共有12个小题,每小题5分,共60分。每小题给出的四个选项中,只有一项是符合要求的。
1.下列集合中,不同于另外三个集合的是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2. 设集合![]() ,
,![]() ,则
,则![]()
(A)![]() (B)
(B)![]()
(C) ![]() (D)
(D) ![]()
3.下列命题中,对于命题![]() 的说法正确的是
的说法正确的是
(A)![]() 且
且![]() 为假 (B)
为假 (B)![]() 或
或![]() 为假 (C) 非
为假 (C) 非![]() 为真 (D) 非
为真 (D) 非![]() 为假
为假
4.已知函数![]() 的图象过点
的图象过点![]() ,则
,则![]() 的反函数的图象过点
的反函数的图象过点
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5.等差数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,则
,则![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
6.等差数列![]() 共
共![]() 项,其中奇数项的和为90,偶数项的和为72,且满足
项,其中奇数项的和为90,偶数项的和为72,且满足![]() ,则该数列的公差为
,则该数列的公差为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
7.某商品零售价2007年比2006年上涨20%,欲控制2008年比2006年上涨5%,则2008年比2007年应降价
(A)15% (B)12.5% (C)10% (D)5%
8.已知函数![]() 是
是![]() 上的增函数,
上的增函数,![]() 是其图象上的两个点,则不等式
是其图象上的两个点,则不等式![]() 的解集是
的解集是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D) ![]()
9.已知![]() 在
在![]() 上是关于
上是关于![]() 的减函数,则
的减函数,则![]() 的取值范围为
的取值范围为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10.等差数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,那么下列不等式中成立的是
,那么下列不等式中成立的是
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
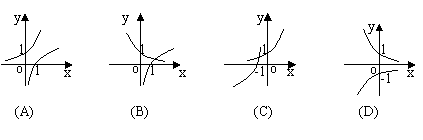
11.已知![]() 且
且![]() ,则在同一坐标系中,函数
,则在同一坐标系中,函数![]() 与
与![]() 的图象只可能是
的图象只可能是
 |
12.从2004年到2007年期间,小王每年8月1日都到银行存入![]() 元的一年定期储蓄,若每年利率为
元的一年定期储蓄,若每年利率为![]() ,且计算复利,到2008年8月1日,小王去取回存款,则可取回本息多少元
,且计算复利,到2008年8月1日,小王去取回存款,则可取回本息多少元
(A)![]() (B)
(B) ![]()
(C)![]() (D)
(D) ![]()
高一上期期末考试
数 学 2008.1
第Ⅱ卷(非选择题,共90分)
注意事项
1.第Ⅱ卷共6页,用钢笔或圆珠笔直接答在试题卷中。
2.答卷前将密封线内项目填写清楚。
|
| 第Ⅰ卷 | 第Ⅱ卷 | 总分 | 总分人 | ||||||
| 题号 | 一 | 二 | 三 | |||||||
| 17 | 18 | 19 | 20 | 21 | 22 | |||||
| 得分 |
|
|
|
|
|
|
|
|
|
|
| 得分 | 评卷人 |
|
|
|
二、填空题(本大题共4小题,每小题4分,共16分,将正确答案填在试题的横线上)
13.![]() ____________.
____________.
14.若不等式![]() 对于一切
对于一切![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是_______________.
的取值范围是_______________.
15.等比数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,则
,则![]() ___.
___.
16.已知函数![]() 的图象与函数
的图象与函数![]() 的图象关于直线
的图象关于直线![]() 对称,则函数
对称,则函数![]() 的单调增区间是________________.
的单调增区间是________________.
三、解答题(本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤)
| 得分 | 评卷人 |
|
|
|
17.(本题满分12分)
设集合![]() ,
,![]() ,
,![]() ,且
,且![]() ,求实数
,求实数![]() ,
,![]() 的取值范围.
的取值范围.
| 得分 | 评卷人 |
|
|
|
18.(本题满分12分)
已知函数![]()
(1) 求函数![]() 的值域;
的值域;
(2) 求函数![]() 的反函数
的反函数![]() ;
;
(3) 证明![]() 在
在![]() 上为减函数.
上为减函数.
得分 | 评卷人 |
|
|
|
19.(本题满分12分)
在等比数列![]() 中,前
中,前![]() 项和为
项和为![]() .命题:若
.命题:若![]() 成等差数列,则
成等差数列,则![]() 成等差数列.
成等差数列.
(1) 写出这个命题的逆命题;
(2) 讨论这个逆命题的真假,并说明理由.
| 得分 | 评卷人 |
|
|
|
20.(本题满分12分)
占地218公顷的世博园,在世博会后作为一个旅游景点吸引四方宾客.按规定,旅游收入除上缴25%的税收外,其余部分自负盈亏.目前,世博园工作人员维持在800人,每天运营成本为29万元(不含工作人员的工资),旅游人数![]() (人)与人均消费额
(人)与人均消费额![]() (元)的关系为
(元)的关系为![]() ,要使工作人员每人每天的工资不低于50元,且维持每天正常运营(不负债),每天的游客应当不少于多少人?
,要使工作人员每人每天的工资不低于50元,且维持每天正常运营(不负债),每天的游客应当不少于多少人?
| 得分 | 评卷人 |
|
|
|
21本题满分12分)
已知二次函数![]()
![]() 满足
满足![]() ,且关于
,且关于![]() 的方程
的方程![]() 的两个实数根分别在区间
的两个实数根分别在区间![]() 内.
内.
(1) 求实数![]() 的取值范围;
的取值范围;
(2) 若函数![]() 在区间
在区间![]() 上具有单调性,求实数
上具有单调性,求实数![]() 的取值范围.
的取值范围.
| 得分 | 评卷人 |
|
|
|
22本题满分14)
二次函数![]() 的图象过原点,将
的图象过原点,将![]() 的图象向左平移1个单位,再向下平移1个单位,得到函数
的图象向左平移1个单位,再向下平移1个单位,得到函数![]() 的图象,且
的图象,且![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,点
,点![]() 均在函数
均在函数![]() 的图象上.
的图象上.
(1) 求数列![]() 的通项公式;
的通项公式;
(2) 设![]() ,
,![]() 是
是![]() 的前
的前![]() 项和,求证:
项和,求证:![]() .
.
高一上期期末测试
数学参考答案 2008.1
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | D | D | A | B | B | B | B | B | D | C | D |
二、填空题:
| 13. | 14. | 15. | 16. |
| 2 |
| 16 |
|
三、解答题:
17. [解]
![]() ………………………………………………………………………1’
………………………………………………………………………1’
![]()
又![]() ………………………………………………………3’
………………………………………………………3’
![]() ………………………………4’
………………………………4’
若![]() ,则
,则![]() ; ………………………………………………………5’
; ………………………………………………………5’
若![]() ,则
,则![]() ………………………………………………………6’
………………………………………………………6’
又![]() ……………………………………………………7’
……………………………………………………7’
若![]() ,则
,则![]() ; ………………………………9’
; ………………………………9’
若![]() ,则
,则![]() ,此时
,此时![]() ,满足
,满足![]() ;…………………………10’
;…………………………10’
若![]() ,则
,则![]() ,此时
,此时![]() ,不满足
,不满足![]() ; ………11’
; ………11’
故![]() 或3,
或3,![]() .
…………………………………………12’
.
…………………………………………12’
18. [解]
(1)由![]() …………………………………1’
…………………………………1’
![]()
即![]() 的值域为
的值域为![]() .…………………………………………3’
.…………………………………………3’
(2)由![]()
![]() ………………………………………………………5’
………………………………………………………5’
![]() . …………………………………………………6’
. …………………………………………………6’
(3)证明:设![]() ,则 ……………………………………………7’
,则 ……………………………………………7’
![]()
![]()
![]()
![]() ………………………………………………9’
………………………………………………9’
![]()
故![]() ………………………………………11’
………………………………………11’
所以,![]() 在
在![]() 上为减函数.……………………………………12’
上为减函数.……………………………………12’
19. [解]
(1)逆命题:若![]() 成等差数列,则
成等差数列,则![]() 成等差数列.……3’
成等差数列.……3’
(2)设![]() 的首项为
的首项为![]() ,公比为
,公比为![]()
由已知得![]()
![]() ………………………5’
………………………5’
当![]() 时,
时,![]() ,
,
不能使![]() 成等差数列; …………………………………………8’
成等差数列; …………………………………………8’
当![]() 时,
时,![]() ……………9’
……………9’
![]() ……………………………10’
……………………………10’
![]() ,能使
,能使![]() 成等差数列. ………………………11’
成等差数列. ………………………11’
综上所述:当![]() 时,逆命题为假;
时,逆命题为假;
当![]() 时,逆命题为真.………………………………12’
时,逆命题为真.………………………………12’
20. [解]要使工作人员每人每天的工资不低于50元,且维持每天正常运营,即每天的旅游收入除上缴税收后不低于290000+800×50=330000元. ……………………………………………………………………………2’
由![]() ……………………………………6’
……………………………………6’
![]() …………………………………………….7’
…………………………………………….7’
![]() …………………………………………………9’
…………………………………………………9’
又由![]() =60t–22900
=60t–22900![]() 0得
0得![]()
![]()
![]() …………………………………………………………10’
…………………………………………………………10’
当![]() 时,
时,![]() …………………………11’
…………………………11’
即要维持每天正常运营,每天的游客应当不少于1100人. …………12’
21. [解]
(1)由![]() …………………………1’.
…………………………1’.
记![]()
由题可知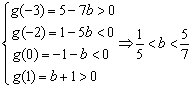
即![]() . …………………………………………………………6’
. …………………………………………………………6’
(2)令![]()
![]()
![]() ,
,![]() 在区间
在区间![]() 上是减函数.………………7’
上是减函数.………………7’
而![]() ,函数
,函数![]() 的对称轴为
的对称轴为![]() ,
,
![]() 在区间
在区间![]() 上单调递增. …………………………………8’
上单调递增. …………………………………8’
故要满足条件,只需![]() 在区间
在区间![]() 上恒有
上恒有![]()
即只需![]() . ……………………………………………………10’
. ……………………………………………………10’
又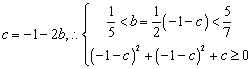
![]() . …………………………………………………………12’
. …………………………………………………………12’
22. [解]
(1)![]() 过原点,所以可设
过原点,所以可设![]() ,则 ……………1’
,则 ……………1’
![]()
由![]()
![]() .…………………………………………………3’
.…………………………………………………3’
故![]() .…………………………………………………………4’
.…………………………………………………………4’
又点![]() 在
在![]() 上
上![]() ………………………5’
………………………5’
当![]() 时,
时,![]() …………………………………………7’
…………………………………………7’
当![]() 时,
时,![]() ,适合上式.
,适合上式.
所以![]() .…………………………………………………8’
.…………………………………………………8’
(2)![]() ……………10’
……………10’
所以![]()
![]()
![]() ………………………………………………………12’
………………………………………………………12’
![]()
![]() . …………………………………………………………………14’
. …………………………………………………………………14’