高一数学必修1练习题(一)
A组题(共100分)
一、选择题:本大题共5题,每小题7分,共35分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列命题正确的是 ( )
A.很小的实数可以构成集合。
B.集合![]() 与集合
与集合![]() 是同一个集合。
是同一个集合。
C.自然数集![]() 中最小的数是
中最小的数是![]() 。
。
D.空集是任何集合的子集。
2.下列给出函数![]() 与
与![]() 的各组中,是同一个关于x的函数的是 ( )
的各组中,是同一个关于x的函数的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3. 设集合P={ xx=2n+1,n![]() 则P、Q的关系是( )
则P、Q的关系是( )
A.![]() B.
B.![]() , C.
, C.![]() , D.
, D. ![]()
![]()
4.方程![]() 的解集为M,方程
的解集为M,方程![]() 的解集为N,且M∩N={2},
的解集为N,且M∩N={2},
那么![]() ( )
( )
A. 21 B.8 C. 7 D. 6
5.函数![]() 的最大值是 ( )
的最大值是 ( )
A.3 B.4 C.5 D.6
二.填空题:本大题共4小题,每小题6分,共24分.
6.用集合表示图中阴影部分:(填空题)
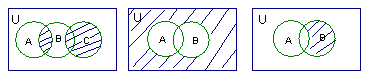
7.设![]() 是锐角},B=(0,1),从A到B的映射是“求余弦”,与A中元素
是锐角},B=(0,1),从A到B的映射是“求余弦”,与A中元素![]() 相对应的B中的元素是 ,与B中元素
相对应的B中的元素是 ,与B中元素![]() 相对应的A中的元素是 .
相对应的A中的元素是 .
8.函数![]() 的定义域为 .
的定义域为 .
9.若全集![]() ,则集合
,则集合![]() 的真子集共有 个.
的真子集共有 个.
三.解答题:本大题共3小题,共41分,解答题应写出文字说明.证明过程或演算步骤.
10.已知集合![]() ,试用列举法表示集合
,试用列举法表示集合![]() .
.
11.若集合![]() ,
,![]() ,求(1)
,求(1)![]() (2)
(2)![]()
12.自行车保管站在某个星期日保管的自行车共有3500辆,其中变速车保管费是每辆一次0.5元,普通车保管费是每次一辆0.3元.
(1)若设普通车停放的辆次数为x,总的保管费收入为y元,试写出y关于x的函数关系式;
(2)若估计前来停放的3500辆次自行车中,变速车的辆次不小于总数的25%,但不大于总数的40%,试求该保管站这个星期日收入保管费的范围.
B组题(共100分)
四.选择题:(每小题7分,共35分)
13. 设S={![]() 为 ( )
为 ( )
A.![]() B.{1,3} C.{x=1,x=3} D.{1,2,3}
B.{1,3} C.{x=1,x=3} D.{1,2,3}
14.若集合![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的值为( )
的值为( )
A. ![]() B.
B.![]() C.
C. ![]() 或
或![]() D.
D. ![]() 或
或![]() 或
或![]()
15.已知集合![]() ,则实数a的取值范围是(
)
,则实数a的取值范围是(
)
A. ![]() B.
B.![]() C.
C. ![]() D.
D.![]()
16.若![]() 则求
则求![]() 的值为( )
的值为( )
A.2 B.-5 C.-8 D.8
17.用固定的速度向右图形状的瓶子中注水,则水面的高度h和时间t之间的关系是


五.填空题:本大题共4小题,每小题6分,共24分.
18.![]() =
=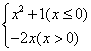 ,若
,若![]() =10,则x= .
=10,则x= .
19.已知函数![]() 的定义域为M,
的定义域为M,![]() 的定义域为N,则
的定义域为N,则![]() 。
。
20.已知![]() =
=![]() ,则
,则![]() 。
。
21.某班有学生![]() 人,其中体育爱好者
人,其中体育爱好者![]() 人,音乐爱好者
人,音乐爱好者![]() 人,还有
人,还有![]() 人既不爱好体育也不爱好音乐,则该班既爱好体育又爱好音乐的人数为
。
人既不爱好体育也不爱好音乐,则该班既爱好体育又爱好音乐的人数为
。
六. 解答题:本大题共3小题,共41分,解答题应写出文字说明.证明过程或演算步骤.
22.含有三个实数的集合可表示为{a,![]() ,也可表示为{
,也可表示为{![]() 求
求![]() 的值.
的值.
23.已知x∈R,集合A={![]() },B={
},B={![]() },
},
若A∩B=B,求实数m的取值范围.
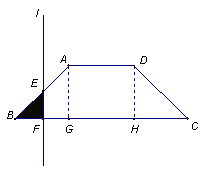 24.如图,已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2
24.如图,已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2![]() cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.
cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.
C组题(共50分)
七.选择题:本大题共2题.每小题7分,共14分.在每小题给出的四个选项中,只有一项是符合题目要求的.
25.已知![]() , 则不等式
, 则不等式![]() 的解集为 (
)
的解集为 (
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
26.设S是至少含有两个元素的集合,在S上定义了一个二元运算“*”(即对任意的![]() ,对于有序元素对(a,b),在S中有唯一确定的元素a*b与之对应).若对任意的
,对于有序元素对(a,b),在S中有唯一确定的元素a*b与之对应).若对任意的![]() ,有
,有![]() ,则对任意的
,则对任意的![]() ,下列等式中不恒成立的是
,下列等式中不恒成立的是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
八.解答题:本大题共2小题,解答题应写出文字说明.证明过程或演算步骤.
27.已知二次函数![]() 同时满足下列条件:(1)
同时满足下列条件:(1) ![]() ,(2)
,(2)![]() 的最大值15,(3)
的最大值15,(3)![]() 的两根立方和等于17,求
的两根立方和等于17,求![]() 的解析式.
的解析式.
28.上因特网的费用由两部分组成:电话费和上网费,以前,上海地区通过“上海热线”上因特网的费用为电话费0.12元/3分钟 ,上网费0.12元/分钟 ,根据信息产业部调整因特网资费的要求,自1999年3月1日起,上海地区上因特网的费用调整为电话0.16元/3分钟 ,上网费每月不超过60小时,以4.00元/小时计算,超过60小时部分,以8.00元/小时计算.
(1)根据调整后的规定,将每月上因特网的费用表示为上网时间(小时)的函数;(每月按30天计算)
(2)某网民在其家庭经济预算中一直有一笔每月上网60小时的费用支出,因特网资费调整后,若要不超过其家庭经济预算中上网费的支出,该网民现在每月可上网多少小时?
(3)从涨价和降价的角度分析上海地区调整前.调整后上因特网的费用情况.
厦门市2007—2008学年数学必修1练习(一)
参考答案
A组
一、1—5:DCCAB
二、6.![]() 7.
7.![]()
8.![]() 且
且![]() } 9.7
} 9.7
三.10.解:由题意可知![]() 是
是![]() 的正约数,当
的正约数,当![]() ;当
;当![]() ;
;
当![]() ;当
;当![]() ;
;
而![]() ,∴
,∴![]() ,即
,即 ![]() ;
;
11.![]()
![]() }
}
12.![]()
![]() (
(![]() )
)
(2)设变速车的辆次为x,
则![]() 即
即![]()
![]()
又![]() 即
即![]()
![]()
B组
一.13—17 BCADB
二.18.-3 19.![]() 20.
20.![]() 21.26
21.26
三.22.依题意:![]() 且
且![]()
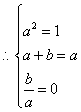 或
或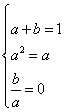 ,解得:
,解得:![]() 或
或![]() (舍去)
(舍去)
![]()
23. ![]()
24.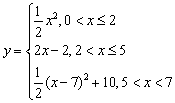
C组
一.25.D 26.A
二.27.![]()
28.调整后
(1)设上网时间为t小时,费用为y元,
则由题意![]()
![]()
即![]()
(2) 因为调整前60小时费用总支出为![]() 元,
元,
调整后若使用60小时,即t=60小时时,费用y=![]() 元,
元,
令576=11.2t-240,解得t=72.85小时.
所以若要调整后不超支,该网民现在每月可上网72.85小时
(3)原来每小时总费用0.12![]() 元
元
![]() 原来总费用y与时间t(小时)函数关系为y=9.6t
原来总费用y与时间t(小时)函数关系为y=9.6t
令11.2t-240=9.6t,解得t=150小时
![]() 当一网民每月上网时间 t<150小时时,调整后支出少,属降价
当一网民每月上网时间 t<150小时时,调整后支出少,属降价
当一网民每月上网时间 t=150小时时,前后支出相同
当一网民每月上网时间 t>150小时时,调整后支出多,属涨价 分
答:(略)
说明:
A组题:最基本要求.最高达到会考的中等要求,与课本的练习题.简单的习题对应.
B组题:中等要求.会考的中.高级要求,高考的中等要求,与课本的习题对应
其中:第16题为2007年福建省高考理科数学第3题原题;
第19题为2007年广东省高考理科数学第1题变式;
第21题为必修一“阅读与思考”的实际应用而设计.
C组题:高等要求.对应高考的高等要求.
其中:26题为2007年广东省高考理科数学第8题原题.