高一数学必修1练习题（二）
A组题（共100分）
一、选择题：本大题共5题，每小题7分，共35分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1． 下列四个函数中，在(0,＋
)上增函数的是 （ ）
A．
＝
B．
C．＝
D．＝-｜x｜
2． 函数
在R上是增函数，则m的取值范围是( )
A． 
B．
C．
D．
3． 函数y=
当
时，函数的值域为(
)
A．
B．
C．
D．
4．下列函数既是奇函数又是偶函数的是（ ）
A．
；
B．
；
C．
D．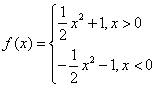
5．定义在R上的函数
对任意两个不等实数a，b，总有
成立，则（ ）
A．函数是先增后减函数 B． 函数是先减后增函数
C．在R上是减函数
D．在R上是增函数
二、填空题：本大题共4小题，每小题6分，共24分．
6 ．函数
，当
是增函数，当
时是减函数，则 m= ．
7．如果函数
，对称轴为
， 则f(1)、f(2)、f(4) 从大到小的顺序是 ．
8．若＝
是偶函数，则的递增区间是
．
9．下列四个结论：①偶函数的图象一定与直角坐标系的纵轴相交；
②奇函数的图象一定通过直角坐标系的原点；
③既是奇函数，又是偶函数的函数一定是＝0（
）；
④偶函数的图象关于y轴对称；
⑤偶函数f(x)在
上单调递减，则f(x)在上单调递增．
其中正确的命题的序号是 ．
三、解答题：本大题共3小题，共41分，解答题应写出文字说明．证明过程或演算步骤．
10．已知是定义在R上的奇函数，且当x＜0时，＝
．求的解析式，并作出的图象．
11．已知函数
．
（1）确定在区间 [3,5]上的单调性并证明；
（2）求的最值．
12．已知定义在（－1,1）上的奇函数，在定义域上为减函数，且
，求实数a的取值范围．
B组题（共100分）
四、选择题：（每小题7分，共35分）
13．设函数
为奇函数，则a =（ ）
A．0 B．1 C．－1 D． 无法确定
14．奇函数y＝，()的图象必过点（ ）
A．（a,-
） B．(－a,) C． (－a,－) D．（a,
）
15．已知函数
在［5,20］上是单调函数，则实数K的取值范围是（ ）
A．
B．
C．［40,160］ D．
16．＝
在区间
上递减，则a的取值范围是（ ）
A．.[－3,
)
B．(
,－3] C． (,5]
D． [3,)
17．是定义在[－6,6]上的偶函数，且
，则下列各式一定成立的（ ）
A．
B．
C．
D．.
五、填空题：本大题共4小题，每小题6分，共24分．
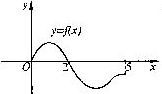
18．设奇函数的定义域为
，若当
时，的图象如右图所示，则不等式
的解是 ．
19．已知
是偶函数，且其定义域为
，则a＝ ，b＝ ．
20．已知与
都是定义在R上的奇函数，若
＝
＋2，且
，则
＝ ．
21．
函数
当x
[-1，3]时有最大值3，则m的值为 ．
六、解答题：本大题共3小题，共41分，解答题应写出文字说明．证明过程或演算步骤．
22．已知
在区间
内有一最大值
，求
的值
23．设函数＝
是奇函数，其中
，
，
．
⑴求
的值；
⑵判断并证明在
上的单调性．
24．某企业为适应市场需求，准备投入资金20万生产W和R型两种产品．经市场预测，生产W型产品所获利润
(万元)与投入资金
(万元)成正比例关系，又估计当投入资金6万元时，可获利润1.2万元．生产R型产品所获利润
(万元)与投入资金
(万元)的关系满足
，为获得最大利润，问生产W．R型两种产品各应投入资金多少万元？获得的最大利润是多少？(精确到0.01万元)
C组题（共50分）
七、选择题：本大题共2题．每小题7分，共14分．在每小题给出的四个选项中，只有一项是符合题目要求的．
25．
已知函数是R上的增函数，A(0,－1)．B(3,1)是其图象上的两点，那么
＜1的解集的补集是（ ）
A．(－1,2)
B． (1,4) C．
D．(
26． 若满足
，且在
上是增函数，又f（-2）=0，则
的解集是（ ）
A． 
B．
C．
D．
八、解答题：本大题共2小题，解答题应写出文字说明．证明过程或演算步骤．
27．设为实数，函数
，
．
（1）讨论的奇偶性；
（2）求的最小值
28．已知函数对任意的x，y
总有
且当x
时，
，
．
（1）求证在R上是奇函数；
（2）求证在R上是减函数；
（3）求在[-3，3]上的最大值和最小值．
厦门市2007—2008学年数学必修1练习（二）参考答案
A组：
一、1－5．CABCD
二、6．－8 7．f(4)>f(1)>f(-2) 8．
9．
④⑤
三、
10．
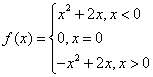，图略
11．增， 最大值为1.5,最小值为1.25
12． 
B组：
四、13－－17．CCDBA
五、18．
19．
20．-1
21．0,7,－2
六、 22．解：对称轴
，
（1）当
即
时，是的递减区间，
则
，得
或
，而，即；
（2）当
即
时，是的递增区间，则
，
得或
，而，即不存在；
（3）当
即
时，
则
，即
；∴或 
23．(1) 由＝是奇函数
得f(-x)+f(x)=0
又f(1)=2
又
又
或1,若a=0则
舍去
(2)增 (略)
24．设生产R型产品应投入资金x万元,则生产W 型产品应投入资金（20－x）万元，
所获总利润为y 万元,设＝K,
令
则
当
即
此时20－x=10.23,y取最大值为
生产W 型产品应投入资金10.23 万元, 生产R型产品应投入资金9.77万元, 可获得的最大利润约为5.95万元
C组：
七、25．D 26．A
八、27．解：（1）当
时，
为偶函数，
当
时，
为非奇非偶函数；
（2）当
时，
当
时，
，
当
时，
不存在；
当
时，
当
时，
，
当
时，
28． (1) 取x=y=0得f(0)=0
取 
是奇函数
（2）设
在R上是减函数
（3）
在[-3,3]上是减函数
又
说明：
A组题：最基本要求．最高达到会考的中等要求，与课本的练习题．简单的习题对应．
其中：第10题为课本P43A组第6题的变式.
第11题为课本P35例4变式
B组题：中等要求．会考的中．高级要求，高考的中等要求，与课本的习题对应．
其中：第15题为课本P489 原题
第18题为2007年宁夏．海南高考第14 题.
C组题：高等要求．对应高考的高等要求．
其中：第27题为福建省 2002年理科高考第21题 .