高一数学必修1练习题(三)
A组题(共100分)
一.选择题:本大题共5题,每小题7分,共35分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列等式能够成立的是( )
A.![]() ,
,![]() B.
B.![]() ,
, ![]()
C.![]() ,
,![]() D.
D. ![]() ,
,![]()
2.化简![]() 的结果是( )
的结果是( )
A.![]() B.
B.![]() C.-1
D.1
C.-1
D.1
3.已知集合M={-1,1},![]() ,则
,则![]() (
)
(
)
A.{-1,1} B.{-1} C.{0} D.{-1,0}
4.函数![]() 的定义域.值域依次是( )
的定义域.值域依次是( )
A.R,R B.R,![]()
C.![]() D.
D. ![]()
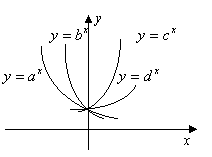 5.如图a,b,c,d都是不等于1的正数,
5.如图a,b,c,d都是不等于1的正数,![]() 在同一坐标系中的图象,则a,b,c,d的大小顺序是( )
A.b<a<d<c B.a<b<d<c
在同一坐标系中的图象,则a,b,c,d的大小顺序是( )
A.b<a<d<c B.a<b<d<c
C.a<b<c<d D.b<a<c<d
二.填空题:本大题共4小题,每小题6分,共24分。
6.某种细菌在培养过程中,每20分钟分裂一次(一个分裂为两个),经过三个小时,这种细菌由1个可繁殖成 .
7.指数函数![]() 在R上是减函数,则a的取值范围 .
在R上是减函数,则a的取值范围 .
8. 若0<x<1,则 ![]() 的大小关系是 .
的大小关系是 .
9.当![]() 时,函数
时,函数![]() 的值域为———.
的值域为———.
三.解答题:本大题共3小题,共41分,解答题应写出文字说明.证明过程或演算步骤.
10.已知![]()
①当x为何值,f(x)=g(x)
②当x为何值,f(x)>1
③当x为何值, 1<g(x)<10
11.已知![]() ,求下列各式的值:⑴
,求下列各式的值:⑴![]() ; ⑵
; ⑵![]() .
.
12.已知![]()
⑴判断f(x) 的奇偶性,并证明之;
⑵利用单调性的定义证明:f(x)是其定义域上的增函数。
B组题(共100分)
四.选择题:(每小题7分,共35分)
13.已知![]() ,
,![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
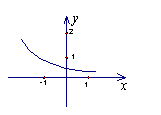 14.函数
14.函数![]() 的图象如图, 其中a.b为常数,则下列结论正确的是( )
的图象如图, 其中a.b为常数,则下列结论正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
15.函数![]() 是指数函数,则有(
)
是指数函数,则有(
)
A.a=1或a=2 B. a=1 C. a=2 D . a>0且a≠1
16. 设f(x)=![]() 那么f(x)是( )
那么f(x)是( )
A.偶函数且在(0,+∞)上是增函数 B.偶函数且在(0,+∞)上是减函数
C.奇函数且在(0,+∞)上是减函数 D.奇函数且在(0,+∞)上是增函数
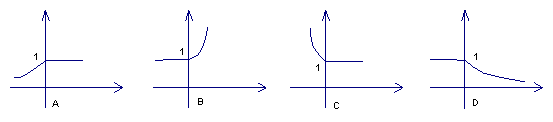
17.定义运算![]() ,则函数
,则函数![]() 的图象是(
)
的图象是(
)

五.填空题:本大题共4小题,每小题6分,共24分.
18.若函数为奇函数,且当x>0时,![]() ,则当x≤0时的解析式为
.
,则当x≤0时的解析式为
.
19.已知![]() 时,函数
时,函数![]() 的值恒大于1,则实数a的范围是 .
的值恒大于1,则实数a的范围是 .
20.设0<a<1,使不等式 ![]() 成立的x的集合是 .
成立的x的集合是 .
21.设![]() 为奇函数,则a的值为 .
为奇函数,则a的值为 .
六. 解答题:本大题共3小题,共41分,解答题应写出文字说明.证明过程或演算步骤.
22. 设![]() ,(其中
,(其中![]() ),确定x为何值时,有:
),确定x为何值时,有:
⑴![]() ⑵
⑵![]()
23.求函数![]() 在
在![]() 上的值域.
上的值域.
24.已知![]() ,
,
⑴求![]() 的定义域
的定义域
⑵判断![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
⑶证明![]()
![]()
C组题(共50分)
七.选择或填空题:本大题共2题。每小题7分,共14分。在每小题给出的四个选项中,只有一项是符合题目要求的。
25. 下列各式中正确的有 (只要求填写正确的序号)
(1)函数![]() 的图象不经过第二象限,则a.b应满足条件
的图象不经过第二象限,则a.b应满足条件![]() ;
;
(2)函数![]()
![]() 的图象恒过定点 (1,2) .
的图象恒过定点 (1,2) .
(3)方程![]() 的实数根的个数为 3个 .
的实数根的个数为 3个 .
(4)函数![]() 的图象与函数
的图象与函数![]() 的图象关于原点对称.
的图象关于原点对称.
(5)函数![]() 在区间[1,2]上的最大值比最小值大
在区间[1,2]上的最大值比最小值大![]() ,则
,则 ![]() .
.
26.函数![]() ,且
,且![]() ,对于
,对于![]() ,有
,有![]() ,则有(
)
,则有(
)
A.![]() >
>![]() B.
B.![]()
![]()
![]()
C.![]() <
<![]() D.
D.![]()
![]()
![]()
八.解答题:本大题共2小题,解答题应写出文字说明.证明过程或演算步骤。
27.画函数![]() 的图象,并根据图象得出k为何值时,关于x的方程
的图象,并根据图象得出k为何值时,关于x的方程![]()
(1)无解?(2)有一解?(3)有两解?
28.设![]() (a为实数),(1)
(a为实数),(1)![]() ,试讨论
,试讨论![]() 的单调性。(2)当a=0时,若函数y=g(x)的图象与y=f(x)的图象关于直线x=1对称,求函数y=g(x)的解析式。
的单调性。(2)当a=0时,若函数y=g(x)的图象与y=f(x)的图象关于直线x=1对称,求函数y=g(x)的解析式。
厦门市2007—2008学年数学必修1练习(三)参考答案
A组:
一.1-5.DCBDA
二.6.512 7.1<a<2 8.![]() 9.
9. ![]()
三.10.①x=0时,f(x)=g(x)=1;② x>0时,f(x)>1;
③ 0<x<1时,1<g(x)<10
11.![]()
12. (1)f(x)为奇函数
![]()
![]() f(x)
f(x)![]()
![]() 为奇函数
为奇函数
(2)f(x)可化为:![]()
由(1)得定义域为![]() 任取
任取![]()
![]()
![]()
![]()
![]() 又
又![]()
![]() .
.![]() 在其定义域为
在其定义域为 ![]() 上是增函数
上是增函数
B组:
四.13--17.BDCBA
五.18.![]() 19.
19.![]() 20.
20.![]() 21.1
21.1
六. 22.(1)![]() 解得
解得![]()
(2)由![]()
![]()
当a>1时![]() 解得x>
解得x>![]()
当0<a<1时![]() 解得x<
解得x<![]()
综上:当a>1时 x>![]() ;当0<a<1时 x<
;当0<a<1时 x<![]() ……
……
23.解:![]()
![]()
而![]() ,则
,则![]()
当![]() 时,
时,![]() ;
当
;
当![]() 时,
时,![]()
∴值域为![]()
24.解:(1)定义域为![]()
(2)![]()
![]() ,
,![]() 为偶函数
为偶函数
(3)![]() ,
,
当![]() ,则
,则![]() ,即
,即![]() ;
;
当![]() ,则
,则![]() ,即
,即![]() ,
,
∴![]()
![]()
七.25.(1)(2)(4) 26. D
八.27.![]() 无解;
无解;![]() 或
或![]() 一解;
一解;![]() 两解
两解
28.(1)当a=0时![]() 在R上递增
在R上递增
当![]() 时
时![]() 在R上是增函数
在R上是增函数
当![]() 时,
时,![]()
① ![]()
又![]() 是增函数,
是增函数,![]() 存在
存在![]() 有
有![]()
即存在两个实数![]() ,但有
,但有![]() 时
时![]() 在R上不单调。
在R上不单调。
② a=1时,![]()
又![]() 是增函数,
是增函数,![]() 存在
存在![]() 有
有![]()
即存在两个实数![]() ,但有
,但有![]() 时
时![]() 在R上不单调
在R上不单调
③ ![]() 时,
时, ![]() 在R上也不单调
在R上也不单调
(2)在函数y=g(x)的图象上取一点P(x,y),点P关于直线x=1的对称点为
Q 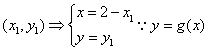 的图象与y=f(x)的图象关于直线x=1对称,
的图象与y=f(x)的图象关于直线x=1对称,![]() 在y=f(x)的图象上,即
在y=f(x)的图象上,即![]() 即
即![]()
说明:
A组题:最基本要求。最高达到会考的中等要求,与课本的练习题.简单的习题对应。
其中:第3题为07山东高考理科试卷第2 题
B组题:中等要求。会考的中.高级要求,高考的中等要求,与课本的习题对应。
其中:第14题05年福建省理科高考试题第6题
第22题为课本P66B组第4 题
C组题:高等要求。对应高考的高等要求。