高一数学必修1练习题(四)
A组题(共100分)
一、选择题:本大题共5小题,每小题7分,共35分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.函数y=lg(2-x)的定义域是 ( )
A.(-∞,2) B. (-∞,2] C.(2,+∞) D. [2,+∞)
2.下列与函数y=x有相同图象的一个函数是 ( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
3. 函数y=log![]() x+log2x2+2的值域是
( )
x+log2x2+2的值域是
( )
A.(0,+∞) B.[1,+∞) C.(1,+∞) D.R
4. 三个数![]() 的大小关系为
(
)
的大小关系为
(
)
A![]()
![]() B
B![]()
![]()
C![]()
![]() D
D![]()
![]()
5. 若f(lnx)=3x+4,则f(x)的表达式为 ( )
A![]() 3lnx B
3lnx B![]() 3lnx +4 C
3lnx +4 C![]() 3ex+4 D
3ex+4 D![]() 3ex
3ex
二、填空题:本大题共4小题,每小题6分,共24分。
6.判断函数![]() 的奇偶性
的奇偶性
![]()
7.幂函数![]() 的图象过点
的图象过点![]() ,则
,则![]() 的解析式是_____________
的解析式是_____________![]()
8.函数y=lgx+lg(x-1)的定义域为A,y=lg(x2-x)的定义域为B,则A、B关系是 .
9.计算:![]() = .
= .
三、解答题:本大题共3小题,共41分,解答题应写出文字说明、证明过程或演算步骤。
10.(本小题13分)计算![]() 的值
的值![]()
11.(本小题14分)求函数y=lgx+lg(x+2)的反函数.
12.(本小题14分)已知函数![]() ,求函数的定义域,并讨论它的奇偶性单调性
,求函数的定义域,并讨论它的奇偶性单调性![]()
B组题(共100分)
四、选择题:本大题共5小题,每小题7分,共35分。在每小题给出的四个选项中,只有一项是符合题目要求的。
13.函数![]() 的定义域是
( )
的定义域是
( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
14.若函数f(x)=logax(0<a<1)在区间[a,2a]上的最大值是最小值的![]() 倍,则a的值为
( )
倍,则a的值为
( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
15. 函数y=lg︱x︱是 ( )
A.偶函数,在区间(-∞,0)上单调递增 B.偶函数,在区间(-∞,0)上单调递减
C.奇函数,在区间(0,+∞)上单调递增 D![]() 奇函数,在区间(0,+∞)上单调递减
奇函数,在区间(0,+∞)上单调递减
16. 已知函数![]() ( )
( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
17. 已知函数![]()
![]() ,则
,则![]() 的值是
( )
的值是
( )
A.9
B.![]() C.-9 D.-
C.-9 D.-![]()
一.填空题:本大题共4小题,每小题6分,共24分。
18.已知![]() 则用a、b表示
则用a、b表示![]()
![]()
19.设![]() ,
, ![]() ,且A=B,则x= ;y=
,且A=B,则x= ;y= ![]()
20. 计算:![]()
![]()
21. 若![]()
上述函数是幂函数的个数是
![]()
五、解答题:本大题共3小题,共41分,解答题应写出文字说明、证明过程或演算步骤。
22.(本小题13分)
已知函数![]()
![]() ,求f(x)的定义域和值域.
,求f(x)的定义域和值域.
23.(本小题14分)已知f(x)=lg(ax-bx)(a,b为常数),
当a>1>b>0时,判断f(x)在定义域上的单调性,并用定义证明.
24.(本小题14分)
求函数![]() 的最小值及取得最小值时自变量x的值.
的最小值及取得最小值时自变量x的值.
C组题(共50分)
六、选择或填空题:本大题共2题。
25.已知y=loga(2-ax)在[0,1]上为x的减函数,则a的取值范围为 ( )
A.(0,1) B.(1,2) C.(0,2) D.[2,+∞)
26.已知x1是方程x+lgx=3的根,x2是方程x+10x=3的根,那么x1+x2的值为( )
A.1 B. 2 C. 3 D.4
七、解答题:本大题共3小题,解答题应写出文字说明、证明过程或演算步骤。
27.已知函数f(x)=log2(x+1),点(x,y)在函数y= f(x)的图象上运动,点(t,s)在函数y=g(x)的图象上运动,并且满足![]()
①求出y=g(x)的解析式.
②求出使g(x)≥f(x)成立的x的取值范围.
③在②的范围内求y= g(x)-f(x)的最小值.
28.设函数y= f(x)是定义在R+上的减函数,并且满足f(xy)= f(x)+ f(y),f(![]() )=1,
)=1,
(1)求f(1)的值,
(2)如果f(x)+ f(2-x)<2,求x的取值范围.
29.已知函数f(x)= loga![]() ,(a>0,a≠1),当x∈(r,a-2)时,f(x)的值域为(1,+∞),求a与r的值.
,(a>0,a≠1),当x∈(r,a-2)时,f(x)的值域为(1,+∞),求a与r的值.
厦门市2007—2008学年数学必修1练习(四)参考答案
A组题(共100分)
一、选择题: ADBDC
二、填空题: 6.(奇函数),7.(![]() ),8.(A
),8.(A![]() B),9.(-2)
B),9.(-2)
三、解答题:
10.解:原式![]()
![]()
11. 解:函数有意义条件是x>0,由x2+2x=10y,∴(x+1)2=10y+1
x+1=![]() ,所求反函数为y=
,所求反函数为y=![]() -1(x∈R)
-1(x∈R)
12. 解:![]() 且
且![]() ,
,![]() 且
且![]() ,即定义域为
,即定义域为![]() ;
;
![]() 为奇函数;
为奇函数;
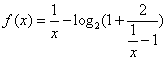 在
在![]() 上为减函数
上为减函数![]()
B组题(共100分)
四、选择题: DABBB
五、填空题: 18.(![]() ),19.(
),19.(![]() ),20.(
),20.(![]() ),21.(2)
),21.(2)
六、解答题:
22.解:![]() ,即定义域为
,即定义域为![]() ;
;
![]() ,即值域为
,即值域为![]()
![]()
23.解:设![]()
![]() f(x)为增函数。
f(x)为增函数。
24. 解:f(x)=(2+lgx)(lgx-1)=(lgx)2+lgx-2=(lgx+![]() )2-2
)2-2![]() ≥-2
≥-2![]() ,
,
∴当x=![]() 时函数取得最小值-2
时函数取得最小值-2![]() .
.
C组题(共50分)
七、选择或填空题: 25.(B),26.(C)
八、解答题:
27.解:①由题意知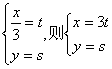
∵点(x,y)在函数y=log2(x+1)的图象上,∴s=log2(3t+1)
即:y=g(x)=log2(3x+1)
②由g(x)≥f(x) 即:log2(3x+1)≥log2(x+1)得
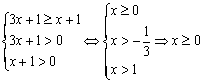
∴使g(x)≥f(x)的x的取值范围是x≥0
③![]()
![]()
![]()
又∵y=log2x在x∈(0,+∞)上单调递增
∴当![]() 即ymin=0
即ymin=0
28.解:①令x=y=1,则f(1)=2f(1),∴f(1)=0;
②有意义条件0<x<2,
又f(x)+f(2-x)=f(2x-x2),2=f(![]() )+ f(
)+ f(![]() )=f(
)=f(![]() )
)
∴f(2x-x2)< f(![]() ),又函数是R+上的减函数,∴2x-x2<
),又函数是R+上的减函数,∴2x-x2<![]()
∴x<1-![]() 或x>1+
或x>1+![]() ,
,
综上x的取值范围是0<x<1-![]() 或1+
或1+![]() < x<2.
< x<2.
29.解: 讨论a>1时,而x<-1,或x>1。函数可拆成y= logat,t=![]() ,y→+∞,t→+∞,x→1, r =1,该条件值+∞要会用;再由单调性得f(a-2)=1,(a>3)a=2+
,y→+∞,t→+∞,x→1, r =1,该条件值+∞要会用;再由单调性得f(a-2)=1,(a>3)a=2+![]() 。
。
0<a<1时,y→+∞,t→0,x→-1,a-2=-1矛盾。∴a=2+![]() ,r =1
,r =1
说明:
A组题:最基本要求.最高达到会考的中等要求,与课本的练习题.简单的习题对应.
B组题:中等要求.会考的中、高级要求,高考的中等要求,与课本的习题对应
C组题:高等要求.对应高考的高等要求.
其中:有些题出自高三复习资料.