高一数学必修1练习题(五)
A组题(共100分)
一.选择题:本大题共5小题,每小题7分,共35分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知函数![]() 唯一的零点在区间
唯一的零点在区间![]() 内,那么下面命题错误的( )
内,那么下面命题错误的( )
A![]() 函数
函数![]() 在
在![]() 或
或![]() 内有零点 B
内有零点 B![]() 函数
函数![]() 在
在![]() 内无零点
内无零点
C![]() 函数
函数![]() 在
在![]() 内有零点
D
内有零点
D![]() 函数
函数![]() 在
在![]() 内不一定有零点
内不一定有零点
2.若![]() ,
,![]() ,则
,则![]() 与
与![]() 的关系是 ( )
的关系是 ( )
A![]()
![]() B
B![]()
![]()
C![]()
![]() D
D![]()
![]()
3. 函数![]() 零点的个数为
( )
零点的个数为
( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
4. 已知函数y=f(x)有反函数,则方程f(x)=0 ( )
A![]() 有且仅有一个根 B
有且仅有一个根 B![]() 至多有一个根 C
至多有一个根 C![]() 至少有一个根 D
至少有一个根 D![]() 以上结论都不对
以上结论都不对
5. 某林场计划第一年造林![]() 亩,以后每年比前一年多造林
亩,以后每年比前一年多造林![]() ,则第四年造林( )
,则第四年造林( )
A![]()
![]() 亩
B
亩
B![]()
![]() 亩 C
亩 C![]()
![]() 亩 D
亩 D![]()
![]() 亩
亩
二.填空题:本大题共4小题,每小题6分,共24分。
6.用“二分法”求方程x3-2x-5=0在区间[2,3]内的实根,取区间中点为x0=2.5,那么下一个有根的区间是
![]()
7.函数f(x)=lnx-x+2的零点个数为
![]()
8. 设函数y=f(x)的图象在[a,b]上连续,若满足 ,则方程f(x)=0在[a,b]上有实根.
9. 若点(2,1)既在函数![]() 的图象上,又在它的反函数的图象上,则
的图象上,又在它的反函数的图象上,则![]() =__________________,
=__________________,![]() =__________________
=__________________![]()
三.解答题:本大题共3小题,共41分,解答题应写出文字说明、证明过程或演算步骤。
10.(本小题13分)
某商品进货单价为![]() 元,若销售价为
元,若销售价为![]() 元,可卖出
元,可卖出![]() 个,如果销售单价每涨
个,如果销售单价每涨![]() 元,销售量就减少
元,销售量就减少![]() 个,为了获得最大利润,则此商品的最佳售价应为多少?
个,为了获得最大利润,则此商品的最佳售价应为多少?
11.(本小题14分)
设![]() 与
与![]() 分别是实系数方程
分别是实系数方程![]() 和
和![]() 的一个根,且
的一个根,且![]() ,求证:方程
,求证:方程![]() 有且仅有一根介于
有且仅有一根介于![]() 和
和![]() 之间。
之间。
12.(本小题14分)
函数![]() 在区间
在区间![]() 上有最大值
上有最大值![]() ,求实数
,求实数![]() 的值
的值![]()
B组题(共100分)
四.选择题:本大题共5小题,每小题7分,共35分。在每小题给出的四个选项中,只有一项是符合题目要求的。
13.如果二次函数y=x2+mx+(m+3)有两个不同的零点,则m的取值范围是( )
A![]() (-2,6) B
(-2,6) B![]() [-2,6] C
[-2,6] C![]() {-2,6} D
{-2,6} D![]() (-∞,-2)∪(6,+∞)
(-∞,-2)∪(6,+∞)
14.已知f(x)=x2-4x-4,当x∈[t,t+1]时函数f(x)的最小值是t的函数,设为g(t),则当t<1时,g(t)等于 ( )
A. t2+2t-7 B. t2-2t+7 C. t2-2t-7 D. t2+2t+7
15. 若函数![]() 在区间
在区间![]() 上的图象为连续不断的一条曲线,则下列说法正确的是( )
上的图象为连续不断的一条曲线,则下列说法正确的是( )
A![]() 若
若![]() ,不存在实数
,不存在实数![]() 使得
使得![]() ;
;
B![]() 若
若![]() ,存在且只存在一个实数
,存在且只存在一个实数![]() 使得
使得![]() ;
;
C![]() 若
若![]() ,有可能存在实数
,有可能存在实数![]() 使得
使得![]() ;
;
D![]() 若
若![]() ,有可能不存在实数
,有可能不存在实数![]() 使得
使得![]() ;
;
16. 设![]() ,用二分法求方程
,用二分法求方程![]() 内近似解的过程中得
内近似解的过程中得![]() 则方程的根落在区间( )
则方程的根落在区间( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]() 不能确定
不能确定
17. 直线![]() 与函数
与函数![]() 的图象的交点个数为( )
的图象的交点个数为( )
A![]()
![]() 个 B
个 B![]()
![]() 个 C
个 C![]()
![]() 个 D
个 D![]()
![]() 个
个
五.填空题:本大题共4小题,每小题6分,共24分。
18.函数![]() 的定义域是
的定义域是
![]()
19.已知函数![]() ,则函数
,则函数![]() 的零点是__________
的零点是__________![]()
20. ![]() 年底世界人口达到
年底世界人口达到![]() 亿,若人口的年平均增长率为
亿,若人口的年平均增长率为![]() ,
,![]() 年底世界人口为
年底世界人口为![]() 亿,那么
亿,那么![]() 与
与![]() 的函数关系式为
的函数关系式为
![]()
21. 若函数![]() 的零点个数为
的零点个数为![]() ,则
,则![]() ______
______![]()
六.解答题:本大题共3小题,共41分,解答题应写出文字说明、证明过程或演算步骤。
22.(本小题13分)证明函数![]() 在
在![]() 上是增函数
上是增函数![]()
23.(本小题14分)借助计算器,用二分法求出![]() 在区间
在区间![]() 内的近似解(精确到
内的近似解(精确到![]() )
)![]()
24.(本小题14分)建造一个容积为![]() 立方米,深为
立方米,深为![]() 米的无盖长方体蓄水池,池壁的造价为每平方米
米的无盖长方体蓄水池,池壁的造价为每平方米![]() 元,池底的造价为每平方米
元,池底的造价为每平方米![]() 元,把总造价
元,把总造价![]() (元)表示为底面一边长
(元)表示为底面一边长![]() (米)的函数
(米)的函数![]() 并求出其最小值.
并求出其最小值.
C组题(共50分)
七.选择或填空题:本大题共2题。
25.在![]() 这三个函数中,当
这三个函数中,当![]() 时,使
时,使![]() 恒成立的函数的个数是 ( )
恒成立的函数的个数是 ( )
A![]()
![]() 个 B
个 B![]()
![]() 个 C
个 C![]()
![]() 个 D
个 D![]()
![]() 个
个
26.函数![]() 与函数
与函数![]() 在区间
在区间![]() 上增长较快的一个是
上增长较快的一个是
![]()
八.解答题:本大题共3小题,解答题应写出文字说明、证明过程或演算步骤。
27.已知![]() 且
且![]() ,求使方程
,求使方程![]() 有解时的
有解时的![]() 的取值范围
的取值范围![]()
28.曙光公司为了打开某种新产品的销路,决定进行广告促销,在一年内,预计年销量Q(万件)与广告费x(万元)之间的函数关系式是Q=![]()
![]() 已知生产此产品的年固定投入为3万元,每生产1万件此产品仍需投入32万元,若每件售价是“年平均每件成本的150%”与“年平均每件所占广告费的50%”之和,当年产销量相等
已知生产此产品的年固定投入为3万元,每生产1万件此产品仍需投入32万元,若每件售价是“年平均每件成本的150%”与“年平均每件所占广告费的50%”之和,当年产销量相等![]() 试将年利润y(万元)表示为年广告费x万元的函数,并判断当年广告费投入100万元时,该公司是亏损还是盈利?
试将年利润y(万元)表示为年广告费x万元的函数,并判断当年广告费投入100万元时,该公司是亏损还是盈利?
29.某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元。
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
厦门市2007—2008学年数学必修1练习(五)参考答案
A组题(共100分)
一.选择题: CACBC
二.填空题: 6.![]() 7.2 8.
7.2 8.![]() 9. a=-3,b=7
9. a=-3,b=7
三.解答题:
10.解:设最佳售价为![]() 元,最大利润为
元,最大利润为![]() 元,
元,
![]()
![]()
当![]() 时,
时,![]() 取得最大值,所以应定价为
取得最大值,所以应定价为![]() 元
元![]()
11.
解:令![]() 由题意可知
由题意可知![]()
![]()
![]()
![]() 因为
因为![]()
∴![]() ,即方程
,即方程![]() 有仅有一根介于
有仅有一根介于![]() 和
和![]() 之间
之间![]()
12.
解:对称轴![]() ,
,
当![]() 是
是![]() 的递减区间,
的递减区间,![]() ;
;
当![]() 是
是![]() 的递增区间,
的递增区间,![]() ;
;
当![]() 时
时![]() 与
与![]() 矛盾;
矛盾;
所以![]() 或
或![]()
![]()
B组题(共100分)
四.选择题:D CCBA
五.填空题: 18.(![]() ),19.(
),19.(![]() ),20.(
),20.(![]() ),21.(4)
),21.(4)
六.解答题:
22.证明:任取![]() ,且
,且![]() ,则
,则![]()
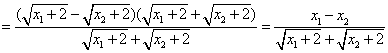
因为![]() ,得
,得![]()
所以函数![]() 在
在![]() 上是增函数
上是增函数![]()
23.解:设在[1,2]上连续f(x)=![]() , f(1)>0, f(2)<0;
, f(1)>0, f(2)<0;
f(1.5)<0,∴解在(1,1.5);
f(1.25)>0,∴解在(1.25,1.5);
f(1.375)<0, ∴解在(1.25,1.375);∴解x≈1.3
24.
解:![]()
![]() (x>0)
(x>0)
y=400(![]() -
-![]() )2+2800≥2800,当x=2时取等号.
)2+2800≥2800,当x=2时取等号.
答:函数![]() (x>0), 当x=2时取得最小值2800元.
(x>0), 当x=2时取得最小值2800元.
C组题(共50分)
七.选择或填空题: 25.(B),26.(![]() )
)
八.解答题:
27.解:![]()
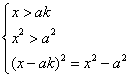 ,即
,即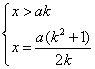
∴![]() ∴
∴![]() <0,
<0,
∴![]() 或
或![]()
28.解:设每年投入x万元,年销量为![]() 万件,每件产品的年平均成本为
万件,每件产品的年平均成本为![]() ,
,
年平均每件所占广告费为![]() ,销售价为
,销售价为![]()
年利润为![]()
![]()
当x=100时,明显y<0![]() 故该公司投入100万元时,该公司亏损
故该公司投入100万元时,该公司亏损![]()
29.解:(Ⅰ)当每辆车的月租金定为3600元时,未租出的车辆数为![]() ,所以这时租出了88辆车.
,所以这时租出了88辆车.
(Ⅱ)设每辆车的月租金定为x元,则租赁公司的月收益为
![]() ,
,
整理得![]() .
.
所以,当x=4050时,![]() 最大,最大值为
最大,最大值为![]() ,
,
即当每辆车的月租金定为4050元时,租赁公司的月收益最大,最大月收益为307050元.
说明:
A组题:最基本要求.最高达到会考的中等要求,与课本的练习题.简单的习题对应.
B组题:中等要求.会考的中、高级要求,高考的中等要求,与课本的习题对应
C组题:高等要求.对应高考的高等要求.
其中:有部分题出自王新敞的资料.