高一年级数学三角函数周末练习（3）
一、选择题
1. 函数f (x)= sin3x的图象的对称中心是（ ）
A、（
k
,0）k
B、（
k
,0）k C、（
k,0）k D、（k,0）k
2.
下列函数中，最小正周期为，且图象关于直线x=
对称的是（ ）
A、y=sin(x +
) B、y=sin(2x +) C、y=sin(2x -)
D、y=sin(2x -)
3.
函数y=sin(
-2x)的增区间是（ ）
A、 [ k-
, k+ 
] k
B、[ k+, k+
] k
C、 [ k-, k+ ] k
D、[ k+, k+
] k
4.
若
为锐角，且sin
<cos
,则满足（ ）
A、> B、< C、+<
D、+>
5.
若tan (2x-)
1,那么x的取值范围是（ ）
A、
B、
C、
D、
6.
要得到函数y=sin(
)的图象，只需将函数y=sin
的图象（ ）
A、向右平移 B、向左平移 C、向右平移 D、向左平移
7.
函数
的单调减区间为（ ）
A .
B.
C.
D.
8.
函数
的最大值是（ ）
A .
B. 
C
. 5 D. 
9.
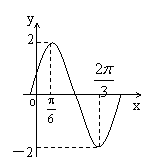函数y＝Asin(ωx＋φ) (A＞0，ω＞0，φ＜
）的图象如图所示，则y的表达式为（ ）
A . y＝2sin(
) B. y＝2sin(
)
C. y＝2sin(2x＋
) D. y＝2sin(2x－)
10. 方程lgx=sinx的解有（ ）
A、1个 B、2个 C、3个 D、4个
二．填空题
11. 已知f(x)=ax+bsinx+1 (a、b 为常数)，且f(5)=7, 则f(-5)=
12. 函数y=(2+sinx)(2-cosx)的最大值
13.
函数y=log0.5cos(x-)的单调递增区间
14.
（1）y=sin(3x+
)-1 （2）y=
以上函数的最大值分别为： ； .
15.
已知f(x)=asinx+btanx+1满足
，
=
16.
曲线
的对称轴为 对称中心为
17.
函数y＝sin＋cos
的最小正周期为
18. 函数y＝x－sinx，x∈［0，π］的最大值为
19.
函数y＝tan（x+
）的定义域为
20.
的单调递减区间为
三．解答题
21.
用五点法作出函数y=sin(-)的图象。
22.
求函数y=tan(-
)的定义域、周期及单调区间
23. 函数y=ksinx+b的最大值为2, 最小值为-4，求k,b的值 k=3 b=-1
24.
已知函数
有最大值
，试求实数
的值
25.
设
满足
,
（１）求的表达式； （２）求的最大值．
周末练习（3）三角函数参考答案（）
一、选择：BDDCCCBBCA
二、填空：
11.-5 12.
13. 
14.0；2 15.-5
16. 
17.
18.
19.
，20. 
三、计算题：
21.略
22
为增区间
23. k=±3；b=-1
24.解：
，对称轴为
，
当
，即
时，
是函数
的递减区间，
得
与矛盾；
当
，即
时，是函数的递增区间，
得
；
当
，即
时，
得
；
25.解：（1）由
①
得
②
由３
①－②，得8
， 故
．（２）对
，将函数的解析式变形，得
＝
， 当
时，