高一年级数学三角函数周末练习（4）
三角函数
一、选择题
1、
的值是（ ）
A、
B、
C、
D、
2、已知集合
，
Z}，
，Z}，则（ ）
A、
B、
C、
D、
3、
，则
的值是（ ）
A、0
B、1
C、
D、
4、如果
是增函数，且
是减函数，那么
的终边在（ ）
A、第一象限 Ｂ、第二象限 Ｃ、第三象限 Ｄ、第四象限
5、是三角形的一个内角，且
，则
的值是（ ）
A、
B、
C、
D、
6、若函数
的图象上每一点的纵坐标保持不变，横坐标伸长到原来的2倍，然后再将整个图象沿轴向左平移
个单位，沿
轴向下平移1个单位，得到函数
的图象，则有是( )
A、
B、
C、
D、
7、满足
的的集合是（ ）
A、
，Z}
B、
，Z}
C、
，Z}
D、
，Z}
，Z}
8、若对任意实数
，函数
（N）在区间[，
]上的值
出现不少于4次且不多于8次，则
的值是（ ）
A、2 B、4 C、3或4 D、2或3
9、若
对任意的实数都有
，则
等于（ ）
A、0
B、3
C、
D、3或
10、
是正实数，函数
在[
，
]上递增，那么（ ）
A、
B、
C、
D、
二、填空题
11、已知函数
的最大值为3，最小值为1，则函数
的最小正周期为_____,值域为____________.
12、函数
的单调减区间是____________________.
13、若
，则
______________.
14、当
[
，
]时，函数
的最小值是_______，最大值是_______.
15、若
，且
是奇函数，则
的值是________________.
16、构造一个周期为
，值域为[，
]，在[0，
上是减函数的偶函数
__.
三、解答题
17、（1）已知
终边上一点
（
，
）（
）,求
，
，
的值；
（2）化简
.
18、求函数
的定义域．
18、求函数
的单调递减区间．
19、若函数
（
）的最小值是
，求实数的值，并求出此时
的最大值.
20、已知定义在区间[
，
]上的函数的图象关于直线
对称，当[
，]时，函数
（
，
，
）的图象如图所示.
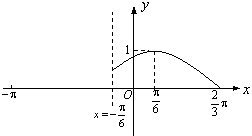（1）求函数在[，]上的表达式；
（2）求方程
的解.
21、设二次函数
（，
R），已知不论、
为何实数，恒有
和
成立.
（1）求证：
；
（2）求证：
；
（3）若函数
的最大值为8，求，
的值.
参考答案：
一、选择题 DBCCC BADDA
二、填空题 11、
， 
12、
13、
14、
，2
15、
16、
三、解答题
17、（1）
时，
，
，
；
时，
，cos=
，．
（2）原式
．
18、（1）
；（2）
．
19、
时；
；
时，
．
20、（1）
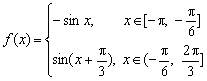；（2）
．
21、（1）（2）略（3）
，
．