高一年级数学下学期期中考试试题
(试卷满分为150分，考试时间为120分钟)
一、选择题(本大题共12小题，每小题5分，共60分)
1
若点P在
的终边上，且OP=2，则点P的坐标（ ）
A．
B．
C．
D．
2.下列函数中，最小正周期为
的是（ ）
A．
B．
C．
D．
3
的值是( )
A． 1
B. 2
C. 4 D.
4．函数
∈
的值域是（ ）
A. 
B. 
C. [－2，2] D. [
]
5．已知
则
值等于 （ ）
A. 
B. 
C. 
D. －7
6. 若三角形的两内角A、B满足sinA·cosB<0,则此三角形必是（ ）
A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 以上情况均有可能
7．函数
的定义域是 （ ）
A. 
B.
C. 
D.
8．函数
的图形的一条对称轴的方程为( )
A. 
B.
C. 
D. 
9.要得到
的图象只要将
的图象经过下列哪种变换得到（ ）
A.向右平移
B.向左平移
C.向左平移
D.向右平移
10.已知
，其中
（-
，
），则（ ）
A.
B.－
C. 
D.
11．已知
的值是（ ）
A． 
B．
C．
2 D． -2
12.函数
上递增，则正实数ω的取值范围是( )
A. 
B. 
C. 
D. 
二、填空题（本大题共4小题，每小题5分，共20分）
13.若点P（
，
）在直线
上，则
的值是__________
14.
是以5为周期的奇函数，
且
则
.
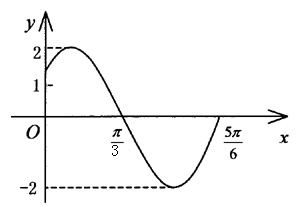
15.右图为函数
图象的一部分，则函数
的解析式为______
__.
16．给出下列命题：
①存在实数，使
；
②若
、
是第一象限角，且
，则
；
③函数
是偶函数；
④函数的图象向左平移个单位，得到函数
的图象．
其中正确命题的序号是____________．（把正确命题的序号都填上）
三、解答题（共70分，要写出必要的文字叙述、演算步骤及推理过程）
17．（10分）已知终边上有一点P（3，
），且 =
，求：
及
，
的值．
18．（12分）不查表求
的值．
19.（12分）求函数
的值域
20．（12分）讨论函数
的定义域、值域、单调性.
21.（12分）已知
的方程
的两个实根，且
，求
的值.
22.(12分)已知函数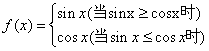
(1)求函数
的值域；
(2)求不等式
的解集；
(3)判断函数是否是周期函数，若是周期函数，指出它的最小正周期，并说明你的理由.
高一年级数学期中试卷(答案)
一、选择题(本大题共12小题，每小题5分，共60分)
1．D 2.B 3.C 4.D 5.D 6.C 7.B 8.A 9.B 10.D 11.A 12.A
二、填空题（本大题共4小题，每小题5分，共20分）
13.-2 14.-4 15. 
16.
③
三、解答题（共70分，要写出必要的文字叙述、演算步骤及推理过程）
17．解：
∴y=±9
当y=9时，
当y=－9时，
18.解：原式=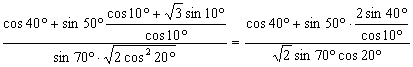
=
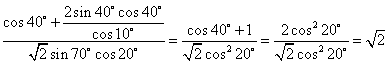
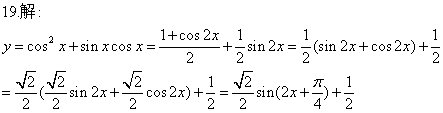
所以原函数的值域为
20．解：
即
又
当
即
时，函数y单调递增，
当
时，函数单调递减.
21.分析：由
、
确定
，由
求得
，
故
22．解：
(1)绘出的图象如图
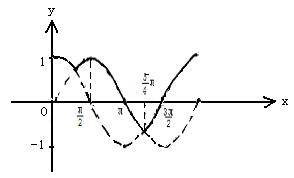
(2)由图象解得
(3)是周期函数，最小正周期
