高一年级数学第三模块学段考试试题
一.选择题(每小题4分,合计40分)
1．任何一个算法都必须有的基本结构是（ ）．
A 顺序结构 B 条件结构 C 循环结构 D 三个都有
2．用秦九韶算法求多项式
在
的值时，其中
的值为（ ）．
A 28 B 8 C -18 D -3
3．在用样本频率估计总体分布的过程中，下列说法中正确的是( )
A.总体容量越大，估计越精确 B.总体容量越小，估计越精确
C.样本容量越大，估计越精确 D.样本容量越小，估计越精确
4．一个容量为20的样本数据，分组后组距与频数如下表.
| 组距 | ［10，20） | ［20，30） | ［30，40） | ［40，50） | ［50，60） | ［60，70） |
| 频数 | 2 | 3 | 4 | 5 | 4 | 2 |
则样本在区间（－∞，50）上的频率为( )
A.0.5 B.0.25 C.0.6 D.0.7
5. 针对甲乙两个班期末数学考试成绩,下列说法正确的是：( )
(A)平均成绩相同，表明这两个班数学学习情况一样
(B)方差甲班比乙班的小，表明甲班的数学学习情况比乙班好
(C)平均成绩甲、乙两班相同，方差甲班比乙班大，则数学成绩甲班比乙班整齐
(D)平均成绩甲、乙两班相同，方差甲班比乙班小，则数学成绩甲班比乙班整齐
6.一组数据的方差是
，将这组数据中的每一个数据都乘以2，所得到的一组新数据的方差是（ ）
Ａ. 
； Ｂ. 
； Ｃ．
； Ｄ． 
7．某人射击5枪，命中3枪，命中的3枪中恰有2枪连中的概率为（ ）
A.
B.
C.
D.
8.某产品分甲、乙、丙三级，其中乙、丙两级均属次品，若生产中出现乙级品的概率为0.03、丙级品的概率为0.01，则对成品抽查一件抽得正品的概率为
A.0.09 B.0.98 C.0.97 D.0.96
9. 从全体3位正整数中任取一数，则此数以2为底的对数也是正整数的概率为A.
B.
C.
D.以上全不对
10..取一根长度为3 m的绳子，拉直后在任意位置剪断，那么剪得两段的长都不小于1 m的概率是.( )
A.
B.
C.
D.不确定
二.填空题(每小题5分,合计25分)
11. 下列程序运行后，输出结果分别是(1)_____________;(2)_______________
（1）a=3 (2) x=100
b=－5 i=1
c=8 DO
a=b x=x+10
b=c i=i+1
PRINT a，b，c LOOP UNTIL x=200
END PRINT i，x
END
12.线性回归方程
=bx+a过定点____
13.（1）将（(2)）转化为十进制的数是_______ ;（2）将53（(8)）转化为二进制的数是__________
14. 在编号为1，2，3，…，n的n张奖券中，采取不放回方式抽奖，若1号为获奖号码，则在第k次（1≤k≤n）抽签时抽到1号奖券的概率为____
15. 在一个边长为3 cm的正方形内部画一个边长为2 cm的正方形，向大正方形内随机投豆(规定豆所在的位置以豆和纸面接触点来计算,且假定接触点在不正方形边上)，则所投的豆落入小正方形内的概率是_____
三.解答题(第16题8分;第17.18.19题每题9分,合计30分)
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
16. 对甲、乙两名自行车赛手在相同条件下进行了6次测试，测得他们的最大速度（m/s）的数据如下表.
画出茎叶图，分别求出甲、乙两名自行车赛手最大速度（m/s）数据的平均数、 标准差，并判断选谁参加比赛更合适,简述理由.
17. 甲、乙两个质地均匀的骰子，各个面上分别刻有1，2，3，4，5，6六个数字，将这两个骰子同时掷一次.
（1）若甲面向上的数字为十位数，乙面向上的数字为个位数，问可以组成多少个不同的两位数，其中个位数字与十位数字均相同的数字的概率是多少?
（2）两个骰子面向上的数字之和共有多少种不同结果?面向上数字之和为6的共有多少种情况?计算面向上的数字之和为6的概率.
18. 某水产试验厂实行某种鱼的人工孵化，10000个鱼卵能孵出8513尾鱼苗，根据概率的统计定义解答下列问题：
（1）求这种鱼卵的孵化概率（孵化率）；
（2）30000个鱼卵大约能孵化多少尾鱼苗？
（3）要孵化5000尾鱼苗，大概得备多少鱼卵？（精确到百位）
19.老张和小王约定在某周五早晨6时到7时之间在某火车站门前会面，并约定先到者应等候另一个人15分钟，若先到者15分钟内没有遇到另一人,先到者就离去，求两人能在此火车站门前会面的概率。
淮南二中2010届高一年级数学第三模块学段考试答题卷
一.选择题(每小题4分,合计40分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二.填空题(每小题5分;两答案者每对一个给2.5分,合计25分)
11.__________,_____________; 12.______________
13.__________,_____________; 14.______________; 15.______________
三. 解答题(满分35分)
16(本题满分8分).
解:
_____ ______ ____ ____ ___ ___ __ _______ ____ ____ ____ ___ ____ ____
17(本题满分9分,第一问题4分,每二问5分).
解:
18.(本题满分9分,每一问3分)
解
---- ---- ------ ----- --- - ----- -- -- --- --- --- --- ----- -------- --------- ----- ---- ---- --- ------ ----
19(本题9分).
解:
08.4高一数学第三模块数学测验参考答案 一.选择题(每小题4分,合计40分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | C | C | D | D | C | B | D | B | B |
二.填空题(每小题5分;两答案者每对一个给2.5分,合计25分)
11. - 5，8，8; 11 ; 200 12.
;13._ 379(10)_;_101011(2)_
_; 14.__1/n__; 15. _4/9_
16.解：（1）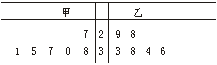
画茎叶图如图 ------3分
=33，
=33；
=3.96，
=3.56；甲与乙的平均速度一样优秀,但乙的发挥较稳定,所以选乙参加比赛较为合适.
------8分
17. 解：（1）甲有6种不同的结果，乙也有6种不同的结果，故基本事件(a,b)总数为36个.---------------1分
其中十位数字共有6种不同的结果，若十位数字与个位数字相同，十位数字确定后，个位数字也即确定.故共有6种不同的结果 -----------2分
即概率为6/36=1/6. -----------4分
（2）两个玩具同时掷的结果(a,b)可能出现的情况共有36种-------5分
出现数字之和为6的共有（1，5），（2，4），（3，3），（4，2），（5，1）
五种情况 -----------7分 所以其概率为5/36. -----------9分
18. 解：（1）这种鱼卵的孵化频率为
=0.8513，它近似的为孵化的概率.
即概率为0.8513 -----------3分
（2）设能孵化x个，则
，∴x=25539，
即30000个鱼卵大约能孵化25539尾鱼苗. -----------6分
（3）设需备y个鱼卵，则
，∴y≈5873，
即大概得准备5873个鱼卵. ------------9分
|
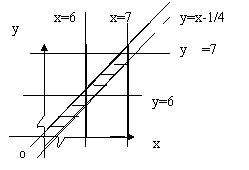19.解:设老张和小王到达的时间分别为x,y(单位:时)则两人能见面必有x-y
1/4,即
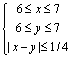,-------3分
在平面直角坐标系中画出此区域 -------------6分
则两人到的时间对(x,y)所在区域面积为1而能见面的时间对(x,y)所在区域面积为7/16,所以能见面的概率问题属于几何概型,所以见面概率为7/16---9分