高一年级数学第二学期周考试题
数学试卷5.30
一、填空题（本大题共14小题，每题5分，共70分）
1．设
是等差数列
的前
项和，若
则
___________.
2．已知
，则
________________.
3．若等差数列的前7项的和为48, 前14项的和为60, 则前21项的和为
4．已知点P（1，2）在
终边上，则
=
。
5.等差数列中，
，若
且
，
，则
的值为________________.
6．已知等差数列的公差
，且a1,a3,a9成等比数列，则
= ；
7．在△OAB中，
=（2cosα，2sinα），
=（5cosβ，5sinβ），若
=-5，则S△OAB= 。
8．若
，则
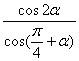值为
。
9．
的三个内角分别为
、
、
，若
和
是关于
的方程
的两实根，则
．
10．在中，
为中线
上一个动点，若
，则
的最小值是
．
11．要得到
的图像，且使平移的距离最短，则需将
的图像
即可得到．
12．小明是戴南高级中学2007级高一学生，为他将来读大学的费用做好准备，他的父母计划从2008年7月1日起至2010年7月1日每月定期到银行存款m元(按复利计算)，2010年8月1日全部取出，月利率按2‰计算，预计大学费用为4万元，那么m=
(计算结果精确到元。可以参考以下数据
)
13．假设实数
是一个等差数列，且满足
及
．若定义
，给出下列命题：①
是一个等比数列；②
；③
；④
；⑤
．其中正确的命题序号为
．
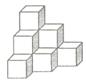14．将棱长相等的正方体按右图所示的形状摆放，从上往下依次为第1层，第2层，第3 层，…，则第6层正方体的个数是
。
二、解答题（本大题共6小题，共90分，解答时应写出文字说明、证明过程或演算步骤）
1５．（本小题1４分，第一、二两小问满分各７分）
已知数列
是等差数列，
是等比数列，且
, 
,(I)求数列
的通项公式；（II）求数列
的前10项和
。
1６．（本小题满分1４分）
在△ABC中，角A、B、C所对的边分别是a、b、c，若
，且
，求△ABC的面积S.
１７.（本小题满分１４分，第一、第二小问满分各７分）
已知函数
（1）写出函数
的最小正周期和单调递增区间；
（2）若
且
，求
的值.
１８.（本小题满分１６分，第一、第二小问满分各8分）在等比数列中，
，公比
，且
，又
与
的等比中项为
，
，数列
的前项和为。
（1）求数列的通项公式。
（2）求
最大值？
1９．（本小题满分１６分）定义：若数列
满足
，则称数列为“平方递推数列”。已知数列
中，
，点
在函数
的图像上，其中为正整数。
（1）证明：数列
是“平方递推数列”，且数列
为等比数列。
（2）设（1）中“平方递推数列”的前项之积为
，即
，求数列的通项及关于的表达式。
（3）记
，求数列
的前项之和，并求使
的的最小值。
２０. (本题满分16分)如图,给出了一个三角形数阵,已知每一列的数成等差数列,从第3行起,每一行的数成等比数列,每一行的公比都相等.记第
行第
列的数为
(
∈N*).
（１）试写出
关于
的表达式,并求
；
（２）设数阵中第n行的所有数之和为An, 求An
(３)这个数阵共有行,求数阵表中的所有数之和.
,
,
,
……
参考答案：
1．
； 2.
； 3. 36； 4．
；5．10；6． 
；7．
； 8． 
；
９.
；
1０．
；1１．向左平移
单位；1２．1569；1３．①②③⑤１４．２１．
1５． 解（I）
是等比数列，且
， 
………3分
……………………７分
（II）数列是等差数列，
，
又
从而
…9分 
……………………1４分
1６． 解：由已知得b2+c2=a2+bc………………………………………………………………2分
…………………………………………………５分
……………………………………………………………７分
由
………………………………………10分
…………………………………………………1４分
17． 解：（1）
周期
…………4分
由
得
的单调增区间为
…………………７分
（2）由，得
，平方得
………９分
又
故
即
………………1２分
，
………………1４分
１8．解：（1）
，
，
又
…………………４分
又与的等比中项为，
而，
…………………６分
，
…………………８分
（2）
是以
为首项，
为公差的等差数列 ………………１０分
………………1４分
当
时，
；当
时，
；当
时，
当
或
时，
最大. ……………………1６分
19．（1）由条件得：
，
，
是“平方递推数列”。
由
为等比数列。
（2）
。 
，
。
（3）
， 
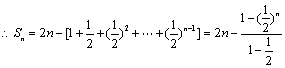
。 由
得
，
当
时，
当
时，
，因此的最小值为1005。
20. 解：(1)由条件易知
第i行的第1个数为ai1=+(i－1)=
,-----------------2分
第i行的第j个数为aij=()j－1,-----------------------4分
∴a83=
×()2=. ----------------------------------6分
(2)设数阵中第n行的所有数之和为An,
则An=
(1++
+…+
)=·
=
－×
.----------9分
（３）设所求数之和为P,则P=(1+2+…+n)－ (1·2－1+2·2－2+…+n·2－n).
设S=1·2－1+2·2－2+3·2－3+…+n·2－n ①------10分
则
=1·2－2+2·2－3+3·2－4+…+n·2－(n+1) ② ----12分
由①-②得
=
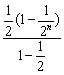－n·2－(n+1)=1－
－
,---------------14分
则P=
－(1－－),=++－1=
+
.
----------------------------------------------------------------------------16分