高一年级数学第二学期期中测试卷
高一年级数学试卷
(考试时间 120 分钟,共 三 大题,满分 150 分) 命题人:黄鹤飞
一、选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的选项中,只有一项是符合题目要求的,把正确答案的序号填入答题卡上的相应空格内。)
1. 角![]() 的终边上有一点
的终边上有一点![]() ,则
,则![]() = ( )
= ( )
A.![]() B.
B. ![]() C.
C.![]() D.
D. ![]()
2.已知![]() ,则
,则![]() 是
是![]() 三点构成三角形的( )
三点构成三角形的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D.既不充分也不必要条件
3.函数![]() 的最小正周期是( )
的最小正周期是( )
A. 2π B. π C. ![]() D.
D. ![]()
4.已知![]() ,则
,则![]() 的值等于( )
的值等于( )
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.设![]() 与
与![]() 是不共线的非零向量,且k
是不共线的非零向量,且k![]() +
+![]() 与
与![]() +k
+k![]() 共线,则k的值是( )
共线,则k的值是( )
A. 1 B. -1 C. ![]() D. 任意不为零的实数
D. 任意不为零的实数
6.在![]() 内,使
内,使![]() 成立的
成立的![]() 的取值范围是
的取值范围是
A.(![]() ) B.(
) B.(![]() ) C.(
) C.(![]() ) D.(
) D.(![]() )
)
7.把函数![]() 的图象向右平移
的图象向右平移![]() 个单位,所得图象关于y轴对称,则
个单位,所得图象关于y轴对称,则![]() 的最小正值为 ( )</PGN0029A.TXT/PGN>
的最小正值为 ( )</PGN0029A.TXT/PGN>
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
8.已知函数![]() 在区间
在区间![]() 上的最小值是
上的最小值是![]() ,则
,则![]() 的最小值等于
( )
的最小值等于
( )
A.
![]() B.
B. ![]() C.
2 D. 3
C.
2 D. 3
|
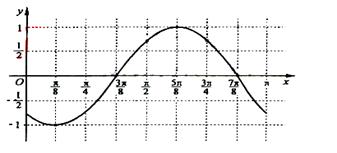
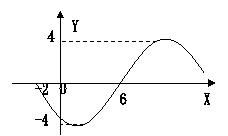 9.函数
9.函数![]() R
R![]() 部分图象如图,则函数
部分图象如图,则函数![]() 的表达式为 ( )
的表达式为 ( )
A.![]() B.
B.![]()
C. ![]() D.
D. ![]()
10.函数![]() 的单调增区间是( )
的单调增区间是( )
A.![]() B.
B. ![]()
C. ![]() D.
D. ![]()
11.已知![]() 是方程
是方程![]() 的两个根,且
的两个根,且![]() 则
则![]() 等于( )
等于( )
A. ![]() B.
B. ![]() 或
或![]() C.
C. ![]() 或
或![]() D.
D. ![]()
12.某学生对函数![]() 进行研究,得出如下四个结论:
进行研究,得出如下四个结论:
①函数![]() 在
在![]() 上单调递增;
上单调递增;
②存在常数![]() ,使
,使![]() 对一切实数
对一切实数![]() 均成立;
均成立;
③函数![]() 在
在![]() 无最小值,但一定有最大值;
无最小值,但一定有最大值;
④点![]() 是函数
是函数![]() 图象的一个对称中心。其中正确的是( )
图象的一个对称中心。其中正确的是( )
A.①③ B.②③ C. ②④ D. ①②④
二、填空题:(本大题共4小题,每小题4分,共16分,请把答案填在答题卡上。)
13.若![]() 则
则![]()
14.已知![]() ,那么
,那么![]()
15.定义运算![]() 为:
为:![]() 例如,
例如,![]() ,则函数
,则函数![]() 的值域为
的值域为
16.给出下列命题:
①存在实数![]() ,使
,使![]() ; ②若
; ②若![]() 是第一象限角,且
是第一象限角,且![]() ,
,![]() ;
;
③函数![]() 是偶函数; ④若
是偶函数; ④若![]() ,则
,则![]() ;
;
⑤将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,得到的是函数
个单位,得到的是函数![]() 的图象。
的图象。
其中正确命题的序号是
|
三、解答题:(本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。)
17.
(本小题满分12分)已知![]() .
.
(1)求![]() 的值; (2) 求
的值; (2) 求![]() 的值.
的值.
18. (本小题满分12分)求函数![]() 的最小正周期、最大值和最小值.
的最小正周期、最大值和最小值.
19.(本小题满分12分)已知![]() 都是钝角,求
都是钝角,求![]() 的值。
的值。
20. (本小题满分12分)设函数![]() 图像的一条对称轴是直线
图像的一条对称轴是直线![]() 。
。
(Ⅰ)求![]() ;
;
(Ⅱ)求函数![]() 的单调增区间;
的单调增区间;
(Ⅲ)用描点法画出函数![]() 在区间
在区间![]() 上的图像。
上的图像。

21. (本小题满分12分)已知函数![]()
(1)设![]() >0为常数,若
>0为常数,若![]() 上是增函数,求
上是增函数,求![]() 的取值范围;
的取值范围;
(2)设集合![]() 若A
若A ![]() B,求实数m的取值范围.
B,求实数m的取值范围.
22. (本小题满分14分)已知:![]() 为常数)
为常数)
(1)若![]() 在[
在[![]() 上最大值与最小值之和为3,求
上最大值与最小值之和为3,求![]() 的值;
的值;
(2)若![]() 时,
时,![]() 有两相异实根
有两相异实根![]() ,求
,求![]() 的取值范围及
的取值范围及![]() 的值。
的值。
|
参考答案:
一、选择题: 1-5 DBCAC 6-10 DBBCA 11-12 DB
二、填空题:13. (5,3) 14. ![]() 15.
15. 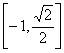 16. ③④
16. ③④
三、解答题:
17.解: (1) 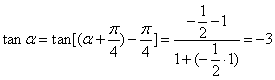 .…………………………6分
.…………………………6分
(2)原式![]()
![]() .…………………………12分
.…………………………12分
18.解:![]()
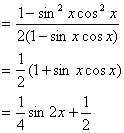
…………………………9分
所以函数f(x)的最小正周期是π,最大值是![]() ,最小值是
,最小值是![]() .…………………………12分
.…………………………12分
19.解![]() …………………………2分
…………………………2分
![]() 都在(
都在(![]() )内,………………… 4分
)内,………………… 4分
于是:![]() …………………………6分
…………………………6分
![]() …………………………8分
…………………………8分
![]() ……………12分
……………12分
20.解:(Ⅰ)![]() 的图像的对称轴,
的图像的对称轴,![]() ……………2分
……………2分
![]()
![]() ………………………4分
………………………4分
(Ⅱ)由(Ⅰ)知![]() ………………………5分
………………………5分
由题意得 ![]() ……………………6分
……………………6分
∴
![]() …………………………7分
…………………………7分
所以函数![]() ……………………8分
……………………8分
(Ⅲ)由![]()
| x | 0 |
|
|
|
|
| ||
| y |
| -1 | 0 | 1 | 0 |
|
|
…………………………12分
21.解:(1)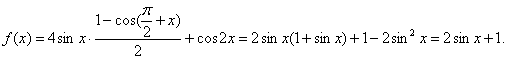 …3分
…3分
|
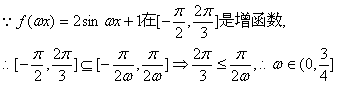
|
|
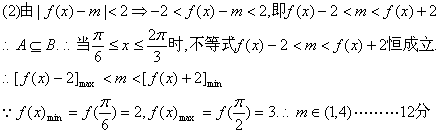
22.解![]() ……………………2分
……………………2分
(1)![]() ………………………3分
………………………3分
![]() …………………………4分
…………………………4分
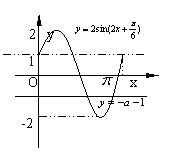 即
即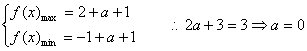 …………6分
…………6分
(2)在同一坐标系内作出![]()
与![]() 的图像(如右图)……………8分
的图像(如右图)……………8分
由图可知:![]() ,且
,且![]()
![]() 且
且![]() ………………10分
………………10分
当![]() 时,
时,![]() ……………12分
……………12分
当![]() 时,
时,![]() 。 ………………………14分
。 ………………………14分