高一年级数学第二学期第一次阶段考试
数 学 试 题
（时间：120分钟 满分: 160分）
一、填空题：本大题共14小题，每小题5分，共70分。不需要写出解答过程，请把答案直接填在答题卡相应位置上。
1.一条直线的倾斜角为
，则该直线的斜率为 ▲
。
2．空间两个角的两边分别平行，则这两个角的大小关系为 ▲ 。
3．下列推理正确的是 ▲ 。（填上所有正确说法的代号）
①
； ②
；
③
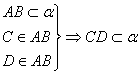； ④
4．在正方体
中，直线
和平面
所成的角为 ▲ 。
5．长方体中，
,则异面直线
与
所成的角为
▲
。
6．在
中，
，
，
,
是平面
外一点，
，则点到平面的距离为 ▲
。
7．若一个正三棱柱的三视图如下图所示，则这个正三棱柱的体积为 ▲ 。
 |
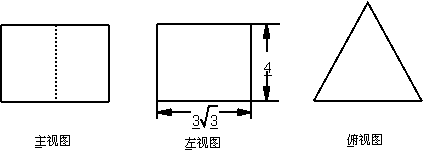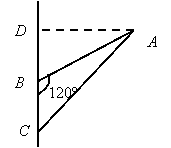8.如图，在中，
,
,若将绕直线
旋转一周，则所形成的旋转体的体积
是 ▲ 。
9．正方体的棱长为
，
为
的中点，则三棱锥
的体积为 ▲ 。
10．下列命题说法正确的是 ▲ 。（填上所有正确说法的代号）
①若直线
与平面
不垂直，则直线不可能垂直于平面内的无数条直线；②两个平面垂直，过其中一个平面内的一点作与它们交线垂直的直线，必垂直于另一个平面；③两组对边分别相等的四边形为平行四边形；④若直线在平面外，则直线与平面至多有一个公共点；⑤过平面外一点作与该平面成
角的直线必有无数多条。
11．过点
作直线，若直线与连结
、
的线段总有公共点，则直线的斜率
的取值范围是
▲
。
12．在半径为
球内有两个平行截面，面积分别为
和
，则此两个平行平面间的距离为 ▲
。
13. 正四面体
中，
分别为棱
上的点，并且
,
设
分别与棱
所成的角为
，则
▲ 。
14．在平面几何里，有勾股定理：“设的两边
互相垂直，则
”.拓展到空间，类比平面几何的勾股定理，研究三棱锥的侧面面积与底面面积的关系，可以得出的正确的结论是：“设三棱锥
的三个侧面
两两互相垂直，则
▲
。”
三、解答题：本大题共6小题，共90分。请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤。
15．（本小题满分12分）
过直线外一点引两条直线
和直线相交于
两点。
求证：三条直线
共面。
16. （本小题满分14分）
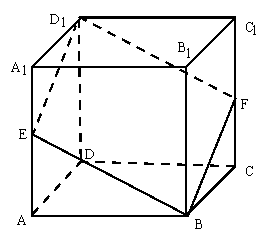已知分别是正方体的棱
上的点，且
,
求证：四边形
是平行四边形。
17. （本小题满分14分）
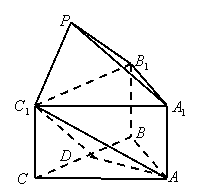如图，正三棱柱ABC—A1B1C1中，AB=2，AA1=1，D是BC的中点，点P在平面BCC1B1内，PB1=PC1=
（I）求证：PA1⊥BC；
（II）求证：PB1//平面AC1D；
18．（本小题满分16分）如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧面PAD⊥底面ABCD，PA=PD，且PD与底面ABCD所成的角为
，
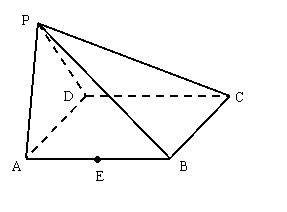（Ⅰ）求证：PA⊥平面PDC；
（Ⅱ）已知E为棱AB的中点，问在棱PD上是否存在一点Q，使EQ∥平面PBC？若存在，写出点Q的位置，并证明你的结论；若不存在，说明理由。
19．（本小题满分16分）在正方体中，分别为
的中点，试问在棱
上能否找到一点
，使
面
?若能，试确定点的位置；若不能，说明理由。
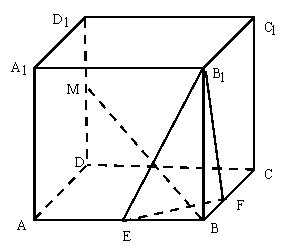
20．（本小题满分18分）
如图所示的空间图形中，已知四边形
、
、
均为矩形，AB1⊥BC1，AB=CC1=1，BC=2。
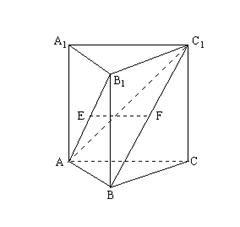⑴设E、F分别为AB1，BC1的中点，求证：EF//平面ABC；
⑵求证：A1C1⊥AB；
⑶求点B1到平面ABC1的距离。
数学试题参考答案
一、填空题：
1. 
2．相等或互补。 3．③④ 4．
5． 
。 6． 
7． 
8. 
9． 
。 10． ④⑤ 11． 
12． 
或
13. 
14． 
三、解答题：（学生提供其它解法请参照给分）
17. （本小题满分14分）
解答：（I）证明：取B1C1的中点Q，连结A1Q，PQ，
∴△PB1C1和△A1B1C1是等腰三角形，∴B1C1⊥A1Q，B1C1⊥PQ，
∴B1C1⊥平面AP1Q，∴B1C1⊥PA1，
∵BC∥B1C1，∴BC⊥PA1.
（II）连结BQ，在△PB1C1中，PB1=PC1=
，B1C1=2，Q为中点，
∴PQ=1，∴BB1=PQ，∴BB1∥PQ，∴四边形BB1PQ为平行四边形，
∴PB1∥BQ. …………6分, ∴BQ∥DC1，∴PB1∥DC1，
又∵PB1
面AC1D，∴PB1∥平面AC1D.
18．（本小题满分16分）解：（1）略
（2）存在 当点Q为PD中点时，EQ∥平面PBC,取PC中点证明BEQF为平行四边形即可。
19． 在棱上能找到一点，使面，且点为棱的中点。
20．（本小题满分18分）
证明：（1）取
的中点
，连接
分别为
的中点,所以
,又
平面,
平面,所以
平面
同理可证:
平面,又
∴平面
平面,又
平面
,所以
平面
(2)连接,四边形为矩形且
,
∴过点且
.又
且
,
∴
平面
,所以
,
又在矩形
中,
,所以
平面,
平面,所以
.
(3) 矩形，∴
又且
，∴
面
又平面ABC1，∴平面ABC1面
又
，
平面ABC1，平面ABC1,∴
平面ABC1
因此点
到平面ABC1的距离就是点B1到平面ABC1的距离。
作
，垂足为，则平面ABC1
∴
就是点到平面ABC1的距离。
在
中， 
，即点B1到平面ABC1的距离为
。