高一数学第二学期期中考试试卷
考试时间90分钟 满分100分
| 题号 | 1—11 | 12—15 | 16 | 17 | 18 | 19 | 20 | 21 | 总分 |
| 得分 |
一.填空题:(![]() )
)
1.计算:![]()
2.函数![]() 的反函数
的反函数![]()
3.若函数![]() 在
在![]() 上是减函数,则
上是减函数,则![]() 的取值范围是
的取值范围是
4.已知 函数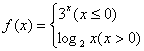 ,那么
,那么![]() =
=
5.若点![]() 是角
是角![]() 终边上的一点,且满足
终边上的一点,且满足![]() ,则
,则![]() =
=
6.设![]() 则
则![]() =
=
7.已知扇形的弧长为![]() ,半径为2,则扇形的圆心角为
,半径为2,则扇形的圆心角为
8.化简:![]() =
=
9.已知函数![]() 且
且![]() 的图像恒过定点P,则P点的坐标是___________
的图像恒过定点P,则P点的坐标是___________
10.函数![]() 且
且![]() 的值域是
的值域是![]() ,则实数
,则实数![]()
11.已知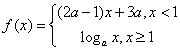 是
是![]() 上的减函数,那么
上的减函数,那么![]() 的取值范围是
的取值范围是
二.选择题:![]()
12.如果![]() 是锐角,那么
是锐角,那么![]() 是( )
是( )
(A)第一象限角 (B)第二象限角
(C)小于![]() 的正角
(D)不大于直角的正角
的正角
(D)不大于直角的正角
13.
“![]() ”是“
”是“![]() ”的( )
”的( )
(A)充分非必要条件 (B)必要非充分条件
(C)充要条件 (D)既非充分又非必要条件
14.今有一组实验数据如下:
|
| 1.95 | 3.00 | 3.94 | 5.10 | 6.12 |
|
| 0.97 | 1.59 | 1.98 | 2.35 | 2.61 |
现准备用下列函数中的一个近似地表示这些数据满足的规律,其中最合适
的一个是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
15.若函数![]() 、三、四象限,则一定有( )
、三、四象限,则一定有( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
三.解答题:(共![]() )
)
16.设函数![]() ,若
,若![]() 求x的取值范围。(
求x的取值范围。(![]() )
)
17.证明恒等式![]() (
(![]() )
)
18.函数![]() ,当
,当![]() 时,求函数的最大值和最小值(
时,求函数的最大值和最小值(![]() ).
).
19.如果光线每通过一块玻璃其强度要减少10%,求至少需要多少块这样的玻璃重叠起来,才能使通过它们的光线强度为原来的强度的![]() 以下?(
以下?(![]() )
)
20.已知函数![]() (
(![]() )
)
(1)
求![]() 的定义域;(
的定义域;(![]() )
)
(2)
判断函数的奇偶性,并加以证明;(![]() )
)
(3)
当![]() 时,求使
时,求使![]() 的x的取值范围。(
的x的取值范围。(![]() )
)
21、已知定义域为![]() 的函数
的函数![]() 是奇函数。(
是奇函数。(![]() )
)
(Ⅰ)求![]() 的值;(
的值;(![]() )
)
(Ⅱ)若对任意的![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围(
的取值范围(![]() )
)
高一数学第二学期期中考试答案
1、4 2、 ![]() (
(![]() )
3、
)
3、 ![]() 4、
4、
![]() 5、
5、![]()
6、 ![]() 7、
7、 ![]() 8、
8、![]() 9、
9、![]() 10、
10、![]() 或
或![]() 11、
11、![]()
12、C 13、B 14、![]() 15、D
15、D
16、![]()
![]() ,
, ![]() 由
由 ![]()
得 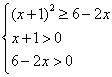 ,解得
,解得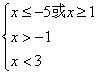 即
即![]()
17、证明:左边=![]() ,=
,=![]()
=![]() ,=
,=![]() =右边
=右边
![]() 等式成立
等式成立
18、解: ![]()
19、解:解:设至少需要重叠n块玻璃
由1×![]()
![]() ,
,![]() ,
,
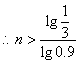 ,
,![]()
答:至少需要重叠11块玻璃
20.解:(1) ![]()
![]() , 即定义域为
, 即定义域为![]()
(2)任取![]()
![]()
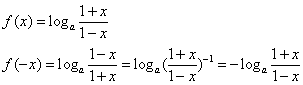
![]() 即
即![]() 是奇函数
是奇函数
(3)![]()
![]() 解得
解得![]()
21、(Ⅰ)因为![]() 是奇函数,所以
是奇函数,所以![]() =0 ,即
=0 ,即![]()
![]() 又由f(1)= -f(-1)知
又由f(1)= -f(-1)知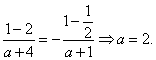
(Ⅱ)解法一:由(Ⅰ)知![]() ,易知
,易知![]() 在
在![]() 上为减函数。又因
上为减函数。又因![]() 是奇函数,从而不等式:
是奇函数,从而不等式: ![]()
等价于![]() ,
,
因![]() 为减函数,由上式推得:
为减函数,由上式推得:![]()
.即对一切![]() 有:
有:![]() ,从而判别式
,从而判别式![]()
解法二:由(Ⅰ)知![]() .又由题设条件得:
.又由题设条件得: ![]() ,
,
即 :![]() ,
,
整理得 ![]()
![]()
上式对一切![]() 均成立,从而判别式
均成立,从而判别式![]()