 高一数学第二学期期中考试试卷
高一数学第二学期期中考试试卷
数 学
得 分_______________
一、填空题:(每小题5分,共70分)
1. ![]() 中
中![]() 则
则![]() 的面积S=___▲ _ ;
的面积S=___▲ _ ;
2. 等差数列![]() 中,
中,![]() ,
,![]() ,那么
,那么![]() ▲ ;
▲ ;
3. 在![]() 中,
中,![]() ,则最大角的余弦值是 ▲ ;
,则最大角的余弦值是 ▲ ;
4. 数列![]() 中,
中,![]() ,则
,则![]() ▲ ;
▲ ;
5. 等差数列![]() 的首项
的首项![]() ,公差
,公差![]() ,如果
,如果![]() 成等比数列,那么
成等比数列,那么![]() 等于 ▲ ;
等于 ▲ ;
6. 已知线段AB两个端点到平面![]() 的距离分别是3和4,则AB的中点到
的距离分别是3和4,则AB的中点到![]() 的距离是 ▲ ;
的距离是 ▲ ;
 7. 已知锐角三角形的边长分别是
7. 已知锐角三角形的边长分别是![]() ,则
,则![]() 的取值范围是 ▲ ;
的取值范围是 ▲ ;
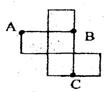
8. 如右图,是一个无盖正方体盒子的表面展开图,A、B、C为其上的三个点,则在正方体盒子中,∠ABC等于_▲________;
 9. 已知x,y满足约束条件
9. 已知x,y满足约束条件 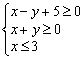 ,则
,则![]() 的最小值为 ▲ ;
的最小值为 ▲ ;
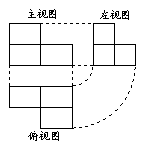
10. 一几何体是由几个相同长方体组成,它的三视图如右,
则此几何体共由___▲___块长方体堆成。
11. 设函数f(x)满足![]() =
=![]() (n∈N*)且
(n∈N*)且![]() ,
,
则![]() = ▲ ;
= ▲ ;
12. 设x>0,y>0,x+y+xy=2,则x+y的最小值是 ▲ ;
 13. 在R上定义运算
13. 在R上定义运算![]() ,若不等式
,若不等式![]()
成立,则实数a的取值范围是___▲ __;
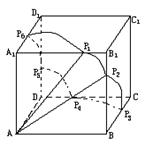
14. 正方体ABCD—A1B1C1D1的棱长为1,在正方体表面上与点A距
离是![]() 的点形成一条曲线,这条曲线的总长度是 ▲ .
的点形成一条曲线,这条曲线的总长度是 ▲ .
陈集中学2007—2008第二学期期中考试试卷
数 学 (答 题 卷)
一、填空题:(共70分)
1、 ; 2、 ;3、 ;
4、 ; 5、 ;6、 ;
7、 ; 8、 ;9、 ;
10、 ;11、 ;12、 ;
13、 ;14、 。
二、解答题(90分)
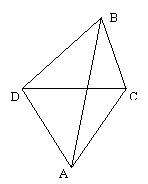
15.(12分)如图,我炮兵阵地位于A处,两观察所分别设于C,D,已知△ACD为边长等于a的正三角形, 当敌目标出现于B时,测得∠CDB=45°∠BCD=75°,且A、B、C、D在同一平面上,我炮兵欲发射炮弹击中目标,则炮弹飞行的距离是多少?(结果保留根式形式)
16. (14分)解关于x的不等式ax2-(a+1)x+1<0.
17. (16分)咖啡馆配制两种饮料,甲种饮料每杯含奶粉9克、咖啡4克、糖3克;乙种饮料每杯含奶粉4克、咖啡5克、糖10克.已知每天原料的使用限额为奶粉3600克、咖啡2000克、糖3000克.如果甲种饮料每杯能获利0.7元,乙种饮料每杯能获1.2 元,每天在原料的使用限额内饮料能全部售出,每天应配制两种饮料各多少杯能获利最大?
18. (16分)如图,三棱柱ABC—A1B1C1的底是边长为![]() 的等边三角形,侧棱与底面垂直,且侧棱长为
的等边三角形,侧棱与底面垂直,且侧棱长为![]() .
.
( 1) 求异面直线AC1与CB1所成的角;
(2) 求AC1与侧面ABB1A1所成的角。


19.(16分)![]() 的三边a、b、c和面积S满足
的三边a、b、c和面积S满足![]() ,
,
 (1)求
(1)求![]() 的值; (2)若
的值; (2)若![]() ,求面积S的最大值。
,求面积S的最大值。
20. (16分)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() =
=![]() ,
,
数列![]() 中,
中,![]() ,点
,点![]() 在直线
在直线![]() 上.
上.
(1)求数列![]() 的通项公式
的通项公式![]() 和
和![]() ;
;
(2) 设![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() ,并求满足
,并求满足![]() 的最大正整数
的最大正整数![]() .
.
数学(答案)
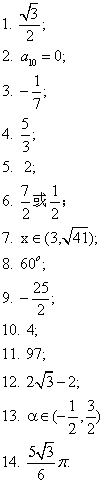
15. 
16. (1)当a=0时,不等式的解集为x>1; ………………………… 2分
(2)当a≠0时,将原不等式分解因式,得a(x-![]() )(x-1)<0 ……………… 4分
)(x-1)<0 ……………… 4分
①当a<0时,原不等式等价于(x-![]() )(x-1)>0,不等式的解集为x>1或x<
)(x-1)>0,不等式的解集为x>1或x<![]() ;…6分
;…6分
②当0<a<1时,1<![]() ,不等式的解集为1<x<
,不等式的解集为1<x<![]() ; ……………………………8分
; ……………………………8分
③当a>1时,![]() <1,不等式的解集为
<1,不等式的解集为![]() <x<1; …………………………10分
<x<1; …………………………10分
④当a=1时,不等式的解为
![]() .
………………………12分
.
………………………12分
综上,当a=0时,不等式的解集为(1,+∞);
当a<0时,不等式的解集为(-∞,![]() )∪(1,+∞);当0<a<1时,不等式的解集为(1,
)∪(1,+∞);当0<a<1时,不等式的解集为(1,![]() );当a>1时,不等式的解集为(
);当a>1时,不等式的解集为(![]() ,1);
,1);
当a=1时,不等式的解集为![]() 。
。
当0<a<1时,不等式的解集为(1,![]() );
);
当a>1时,不等式的解集为(![]() ,1);…………………………………14分
,1);…………………………………14分
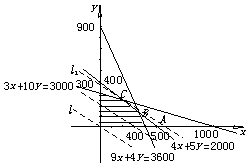 17. 设每天应配制甲种饮料x杯,乙种饮料y杯,获利z元.
17. 设每天应配制甲种饮料x杯,乙种饮料y杯,获利z元.
则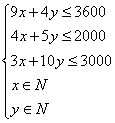 ……………6分
……………6分
目标函数为:z=0.7x+1.2y
作出可行域: ……………10分
作直线l:0.7x+1.2y=0.把直线l向右上方平移至l1的位置时,直线经过可行域上的点C,且与原点距离最大,此时z=0.7x+1.2y取最大值.
解方程组![]()
得点C的坐标为(200,240).
答:每天应配制甲种饮料200杯,乙种饮料240杯,能使该咖啡馆获利最大. …………………16分
18.(1) 在平面ABC内过A作BC的平行线,过B作AC的平行线,交于点D, 连B1D,可得B1C1AD是平行四边形,B1D平行C1A,连CD,可得△B1CD是正△,故异面直线AC1与CB1所成的角是60o. ………8分
(2) 解:取![]() 的中点M,连
的中点M,连![]() ,
,
∵ △A1B1C1是正三角形,∴ MC1⊥A1B1,
又∵ AA1⊥平面A1B1C1,
∴ AA1⊥MC1,
∴ MC1⊥平面ABB1A1
∴ ∠C1AM就是直线AC1与侧面ABB1A1所成的角.
 在
在![]() △AMC1中,
△AMC1中,
![]() ,
,![]() ,
,
∴ ![]() ,
,![]() ,
,
直线AC1与侧面ABB1A1所成的角![]() .…………16分
.…………16分
19. ![]()
由余弦定理得![]()
![]()
又![]()
![]()
![]()
![]() ………… 10分
………… 10分
(2)由上知![]()
![]() ,
,
![]()
![]()
![]() ………… 16分
………… 16分
(或![]() 亦可)
亦可)
20. 解(1)![]()
![]() ………… 2分
………… 2分
![]() .
.
![]()
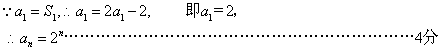
![]()
![]()
(2)![]()
![]() ……9分
……9分
![]()
因此:![]()
即:![]()
![]()
