高一数学第二学期期中联考
高一数学试题卷
命题学校:深圳市第二高级中学 命题教师:陈红明 李爱林
(时间:120分钟 满分:150分)
一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将正确答案的字母填在答题卡的对应题号下)
1、 -215°是
A、第一象限角 B、第二象限角 C、第三象限角 D、第四象限角
2、角![]() 的终边经过点P(7,24),则
的终边经过点P(7,24),则![]() =
=
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、已知向量![]() ,
,![]() 且
且![]() ∥
∥![]() ,则x的值是
,则x的值是
A、-6
B、6 C、![]() D、
D、![]()
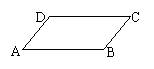 4、如图,在平行四边形ABCD中,下列结论中错误的是
4、如图,在平行四边形ABCD中,下列结论中错误的是
A、![]() =
=![]() B、
B、![]() +
+![]() =
=![]()
C、![]() -
-![]() =
=![]() D、
D、![]() +
+![]() =
=![]()
5、在下面给出的四个函数中,既是偶函数,又是区间![]() 上的增函数的是
上的增函数的是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6、要得到函数![]() 的图象,只需将函数
的图象,只需将函数![]() 的图象上所有点向( )平移( )个单位长度
的图象上所有点向( )平移( )个单位长度
 A、左,
A、左,![]() B、左,
B、左,![]() C、右,
C、右,![]() D、右,
D、右,![]()
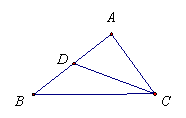
7、如图所示,![]() 是
是![]() 的边
的边![]() 上的中点,则向量
上的中点,则向量![]()
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
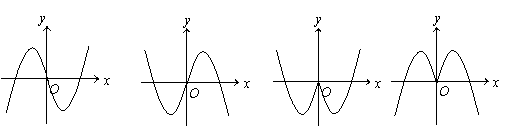 8、函数
8、函数![]() 的部分图象是
的部分图象是
A B C D
二、填空题(本大题共6小题,每小题5分,共30分,请将正确答案填在答题卷相应横线上)
9、cos43°cos77°- sin43°cos13°的值为_________________;
10、已知向量![]() ,
,![]() ,则
,则![]() 的最大值为 ____________;
的最大值为 ____________;
11、化简![]() 的值是_____________;
的值是_____________;
12、已知A(3,-2),B(-6,1),若![]() ,则点P的坐标是_______;
,则点P的坐标是_______;
13、给出下面四个命题:①![]() ;
;
②![]() ;③
;③![]() ;
;
④![]() .
.
其中正确的序号为________;
14、已知![]()
![]() , sin
, sin![]() 则cos
则cos![]() =__________.
=__________.
三、解答题(本大题共6小题,共80分,解答应写出文字、证明过程或演算步骤.请在答题卷上作答)
15、(14分,每小题7分)求值:(1)![]() (2)
(2)![]()
16、(12分)设![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() 共线,试求
共线,试求![]() 的坐标(O为坐标原点).
的坐标(O为坐标原点).
17、(12分)已知![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
18、(14分)已知![]() .
.
(1)求![]() 的夹角
的夹角![]() ; (2)求
; (2)求![]() 的值.
的值.
19.(12分)已知某海滨浴场海浪的高度y(单位:米)是时间t(![]() ,单位:小时)的函数,记作
,单位:小时)的函数,记作![]() .下表是某日各时的浪高数据:
.下表是某日各时的浪高数据:
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
经过长期观测![]() 的曲线可近似地看成是函数
的曲线可近似地看成是函数![]() 的图象.
的图象.
(1)根据以上数据,求函数y的最小正周期T,振幅A及解析式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8:00时至晚上20:00时之间,有多少时间可供冲浪者进行运动?
20、(16分)设![]() ,
,![]() ,记
,记![]() .
.
(1)写出函数![]() 的图象的对称轴方程;
的图象的对称轴方程;
(2)试用“五点法”画出函数![]() 在一个周期内的简图(需列表);
在一个周期内的简图(需列表);
(3)求函数![]() 的单调增区间;
的单调增区间;
(4)设函数![]() (
(![]() ).若
).若![]() 的最小值为2,试求
的最小值为2,试求![]() 的最大值,并指出
的最大值,并指出![]() 取何值时,函数
取何值时,函数![]() 取得最大值.
取得最大值.
2007-2008学年第二学期期中联考
高一数学参考答案
1-8:BCBC DDAA;
9、![]() ;10、
;10、![]() ;11、
;11、![]() ;12、(0,-1);13、①②③;14、
;12、(0,-1);13、①②③;14、![]()
15.解:(1)![]() ……7分
……7分
(2)原式=![]()
=![]() ……14分
……14分
16、解:设![]() ,由题意得:
,由题意得: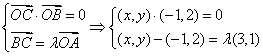 ……6分
……6分
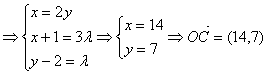 ……12分
……12分
17、解:![]() 且
且![]() ∴
∴![]()
∴原式=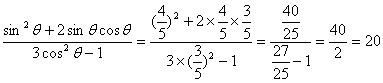 ……………12分
……………12分
18、(1)由![]()
得![]() ,
∴
,
∴![]() ,
,
![]() ……8分
……8分
(2)∵ ![]() ,∴
,∴![]() .……14分
.……14分
19、解:⑴由题可知![]() .
.![]()
![]()
又![]() 。则解析式是
。则解析式是![]() …………………………6分
…………………………6分
⑵由![]() 可得
可得![]() ,
,![]()
即有![]() ,又
,又![]() 得
得![]()
从而共有6小时可供冲浪者进行运动。…………………………12分
20.解:(1)∵![]()
![]()
![]() ,
,
由![]() ,得
,得![]()
即该函数的对称轴方程是![]() ……………4分
……………4分
(1)列表
|
|
|
|
|
|
|
|
| 0 |
|
|
|
|
|
|
|
|
|
|
|
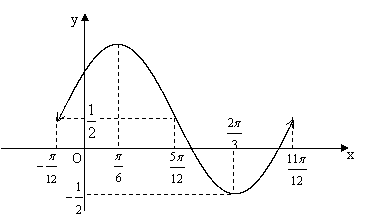 描点连线得函数
描点连线得函数![]() 在一个周期内的简图为
在一个周期内的简图为
………………………8分
(2)函数的单调增区间是![]() ……………………12分
……………………12分
(3)∵
![]() ,∴
,∴ ![]() ,
,
∴ ![]() . 当且仅当
. 当且仅当![]() 时,
时,![]() ,
,
此时,函数![]() 取得最小值
取得最小值![]() ,
,![]() 取最小值
取最小值![]() .
.
即![]() 解得
解得 ![]()
所以, 函数![]() ,∵
,∵![]() ,
,
∴![]() 即
即![]() 时,取得最大值
时,取得最大值![]() ,
,
∴![]() 时,
时,![]() .
……………………16分
.
……………………16分