高一数学第二学期测试卷2008.3
试卷总分100分,考试时间60分钟
一、填空题（每小题5分，共50分）
1、直线
上的点到原点的距离的最小值是
.
2、扇形的圆心角是
，半径为20cm, 则扇形的面积为
3、已知点
在角
的终边上,且满足
,则
的值为 .
4、sin600°的值是 .
5、已知
的值为 .
6、已知
,
,则角所在的象限是 .
7、若cos(π+α)=-
π<α<2π,则sin(2π-α)等于 .
8、先将函数y=5sin（
－3x）的周期扩大为原来的2倍，再将新函数的图象向右平移
，则所得图象的解析式为 .
9、给出下列命题：
①函数
是偶函数；
②函数
在闭区间
上是增函数；
③直线
是函数
图象的一条对称轴；
④将函数
的图象向左平移
单位，得到函数
的图象；
其中正确的命题的序号是： ；
10、圆
关于x轴对称的圆方程是 .
二、解答题（共70分）
11、（本题10分）化简
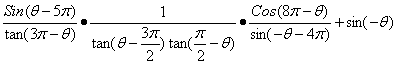
12、（本题15分）已知函数
，设
（1）求函数h(x)的定义域。
（2）判断函数h(x)的奇偶性，并说明理由。
13、（本题15分）（1）已知
，求sinxcosx和sinx-cosx的值。
（2）已知tan=2，求
的值。
14、（本题15分）已知函数f(x)=3sin(2x+)+cos(-2x)-1,
（1）求函数f(x)的最小正周期； （2）求函数f(x)的最大值及取得最大值时x的取值集合;
（3）求函数f(x)的单调递增区间;（4）该函数的图象可以由y=sinx的图象怎样变换得到？
15、（本题15）设函数
的最小值为g(a)
.
⑴求g(a);
⑵求使g(a)
的a的值及此时f(x)的最大值.
高一数学测试卷解答
1、
2、80π cm2
3、
4、
5、-
6、第四象限 7、-
8、 y=5sin（
－
）
9、①③
10、
11、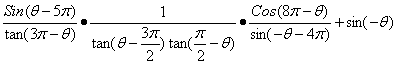
=
=
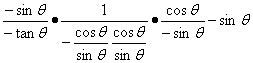12、
13、
解：（1）sinx+cosx=
，
,
sinxcosx= -
;
,
sinx-cosx=
(2)原式=
=
14、解：（1）f(x)=3sin(2x+)+cos(-2x)-1= f(x)=3sin(2x+)+cos[
-（
+2x）]-1
=3sin(2x+)+sin(2x+)-1=4sin(2x+)-1
函数的周期为 T=
=
（2）当 2x+
=
,即
时，
当 2x+=-,即
时，
（3）单增区间：
即
（4）y==sinx 向左平移单位 y=sin(x+) 纵坐标不变，横坐标缩小为原来的一半 y=sin(2x+) 横坐标不变，纵坐标扩大为原来的4倍数 y=4sin(2x+)
向上平移1个单位 y=4sin(2x+)+1
14、解：(1)
=
当
，即
时，
,此时Cosx=-1
当
，即
时，
，此时Cosx=
当>1,即a>2时，
，此时Cosx=1
即g(a)=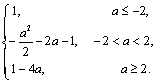
(2) g(a),显然时不合题意
当时，
而
。
当a>2时，1-4a,a
<2,不合题意。
综上所述，所求职a的值为 –1。
a=-1时，