高一数学第二次段考试卷
一.选择题:本大题共10小题;每小题5分,共50分.在每小题给出的四个选项中,有且只有一项是符合题目要求的.
1.若集合M={![]()
![]() },P={
},P={![]()
![]() }, 则M∩P=( )
}, 则M∩P=( )
A.{2,4} B.{4,16} C.{(2,4),(4,16)} D.{![]()
![]() }
}
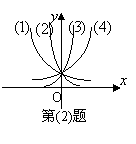
2.如图为指数函数![]() ,则
,则![]() 与1的大小关系为
( )
与1的大小关系为
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
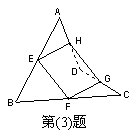
 3.如图,点
3.如图,点![]() 分别为空间四边形
分别为空间四边形![]() 中
中![]() 的中点,若对角线
的中点,若对角线![]() ,且
,且![]() 与
与![]() 成
成![]() ,则四边形
,则四边形![]() 是( )
是( )
A.菱形 B.梯形
C.正方形 D.空间四边形
4.当![]() 时,
时,![]() 、
、![]() 、
、![]() 的大小关系是( )
的大小关系是( )
 A.
A. ![]()
![]()
![]() B.
B.
![]()
![]()
![]()
C. ![]()
![]()
![]() D.无法确定
D.无法确定
5.在空间中,下列四个命题
①两条直线都和同一平面平行,则这两条直线平行;
②两条直线没有公共点,则这直线平行;
③两条直线都和第三条直线垂直,则这两条直线平行;
④一条直线和一个平面内无数条直线没有公共点,则这条直线和这个平面平行
其中正确命题的个数 ( )
A.3个 B.2个 C.1个 D.0个
6.函数![]() 的零点所在的大致区间是( )
的零点所在的大致区间是( )
A.![]() B.
B. ![]() C.
C. ![]() 和
和![]() D.
D. ![]()
7. 已知![]() 是偶函数,定义域为
是偶函数,定义域为![]() .则
.则![]() ,
,![]() 的值分别是 ( )
的值分别是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
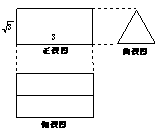
8. 下图是一个几何体的三视图,已知侧视图是一个等边三角形,根据图中尺寸(单位:![]() ),可知这个几何体的表面积是
(
)
),可知这个几何体的表面积是
(
)
A.![]()
B.![]()
 C.
C.![]()
D.![]()
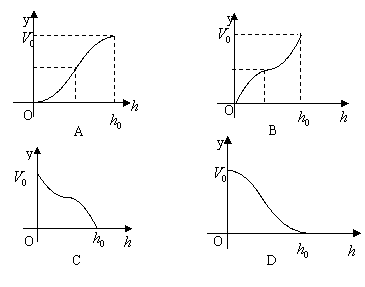
9.一高为![]() 、满缸水量为
、满缸水量为![]() 的鱼缸的轴截面如下图所示,其底部碰了一个小洞,满缸水从洞中流出,若鱼缸水深为
的鱼缸的轴截面如下图所示,其底部碰了一个小洞,满缸水从洞中流出,若鱼缸水深为![]() 时,水的体积为
时,水的体积为![]() ,则函数
,则函数![]() 的大致图象可能是( )
的大致图象可能是( )
 | |||
 | |||
10.设![]() 均为正数,且
均为正数,且![]() ,
,![]() ,
,![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
二. 填空题:本大题共4小题;每小题5分,共20分.
11.已知函数![]() 分别由下表给出:
分别由下表给出:
|
| 1 | 2 | 3 |
|
| 1 | 3 | 1 |
|
| 1 | 2 | 3 |
|
| 3 | 2 | 1 |
则![]() __________;满足
__________;满足![]() 的
的![]() 的值为________
的值为________
12.求函数![]() 的值域是_________________________
的值域是_________________________
13. 设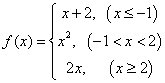 ,若
,若![]() ,则
,则![]() =
=
14.给出下列四个命题:
①函数![]() (
(![]() 且
且![]() )与函数
)与函数![]() (
(![]() 且
且![]() )的定义域相同;
)的定义域相同;
②函数![]() 与
与![]() 的值域相同;③函数
的值域相同;③函数![]() 与
与![]() 在区间
在区间![]() 上都是增函数;④函数
上都是增函数;④函数![]() 与
与![]() 都是奇函数,其中正确命题的序号是_____________(把你认为正确的命题序号都填上)
都是奇函数,其中正确命题的序号是_____________(把你认为正确的命题序号都填上)
三.解答题:本大题6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
15.(本小题满分12分)已知集合![]() ,
,![]() ,
,![]() 求
求![]() 的值.
的值.
16.(本小题满分14分)如图,长方体![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点。
的中点。
(1)求三棱锥![]() 的体积;
的体积;
(2)求证:直线![]() ∥平面
∥平面![]() ;
;
 (3)求证:直线
(3)求证:直线![]()
![]() 平面
平面![]() .
.
17.(本小题满分12分)设二次函数![]() 在
在![]() 上有最大值4,求实数a的值
上有最大值4,求实数a的值
18.(本小题满分14分)甲乙两人连续6年对某县农村鳗鱼养殖业的规模(总产量)进行调查,提供了两个方面的信息,分别得到甲、乙两图:
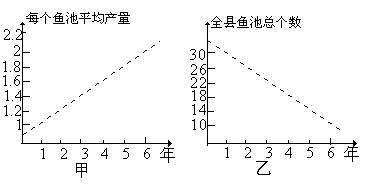
甲调查表明:每个鱼池平均产量从第1年1万只鳗鱼上升到第6年2万只.
乙调查表明:全县鱼池总个数由第1年30个减少到第6年10个.
请你根据提供的信息说明:
(1)第2年全县鱼池的个数及全县出产的鳗鱼总数.
(2)到第6年这个县的鳗鱼养殖业的规模(即总产量)比第1年扩大了还是缩小了?说明理由.
(3)哪一年的规模(即总产量)最大?说明理由.
19.(本小题满分14分)已知函数![]()
(1)求函数![]() 的定义域;
的定义域;
(2)证明:![]() 在(2,+∞)上为增函数;
在(2,+∞)上为增函数;
(3)当![]() 时,求函数的值域.
时,求函数的值域.
20.(本小题满分14分)已知函数![]() 对任意的实数,x,y都有
对任意的实数,x,y都有
![]()
(1)若![]() 试求
试求![]() 的解析式
的解析式
(2)若![]() 且
且![]() 时,不等式
时,不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.