高一数学第十二周每周一考试卷

高一数学第十二周每周一考试卷文科

（集合、不等式的解法、函数）　 命题人：杨昌座

班级：　　　　   姓名：　　　　　　　　  座号：　　　　　　  成绩：　　　　　　

一、选择题：60分

1．己知全集I={1,2,3,4,5}, M ={1,2}, N={1,3,5},则M∩C_IN等于： C

　　 A、{1,2}　　　　  B、{2,3}　　　　  C、{2}　　　　　  D、{2,4}

2．已知集合A=︱}, , 则下列关系正确的是　（　B ）

A. 　　　　B. 　　　 C. 　　　　 D.

3．满足条件{0，1}∪A={0，1}的所有集合A的个数是（　D  ）

A．1个 　　　　　 B． 2个 　　　　　C． 3个 　　　　　D．4个

4．下列各组函数中，表示同一函数的是　C

A．　 B．　 C．　D．

5．函数f(x)=+(x-4)⁰的定义域为： C

　　　A． {xx>2,x≠4}　B、{xx≥2,或x≠4}  C、　D、

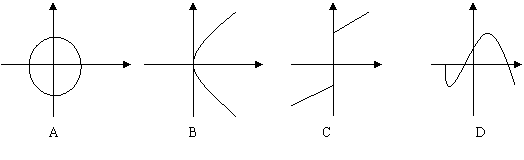
6．下列所示的四幅图中,可表示为y=f（x）的图像的只可能是（　D ）

7．函数y=f（x）的定义域为[－1,2]. 则函数g（x）=f（－x）+f（x）的定义域为（　B ）

A、[－2,2]　　　B．[－1,1]　　　C．[－2,－1]　　　D．[1, 2]

8．已知A、B两地相距150千米，某人开汽车以60千米/小时的速度从A地到达B地，在B地

停留1小时后再以50千米/小时的速度返回A地，把汽车离开A地的距离x表示为时间t（小

时）的函数表达式是（　D　）

A．x=60t  B．x=60t＋50t  C．x=　D．x=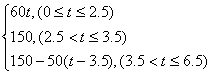

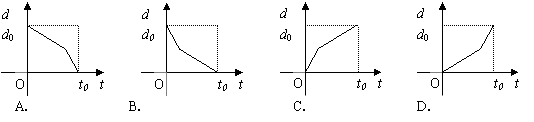9．某学生离家去学校，由于怕迟到，所以一开始就跑步，等跑累了再走余下的路程. 在下图中纵轴表示离家的距离，横轴表示出发后的时间，则下图中的四个图形中较符合该学生走法是（C ）

10．函数y=x²+4x+5(其中x∈[-3,1)的值域为：B

A [2，10）　　 B、[1，10）　　 C、[2，10]　　　 D、[1，10]

11．对于定义在实数集R上的函数f（x）. 如果存在实数x使f（x）= x，则称x叫做函

数f（x）的一个“不动点”.若函数f（x）= x＋ax＋1不存在“不动点”，则a的取值范围（ C　）

A．（－2, 2）　 B．（－∞，－2）∪（2, ＋∞）　　C．（－1, 3）　　 D．（－3, 1）

12．已知恒过定点(2,0)，则的最小值为（　B  ）

 A.5　　　　　　　 B.　　　　　　  C.4　　　　　　　　　  D.

二、填空题：16分

13．用集合表示下图中的阴影部分，则为： 　　(A∩C)∪(B∩C)　(或(A∪B)∩C)　　

14．狄利克莱函数D（x）=，则 =　　　1　　

15．已知集合，，若A∩B=Æ，则实数的取值范

围是: _ {a2≤a≤3}

16．老师给出一个函数y=f（x）.四个学生甲、乙、丙、丁各指出这个函数的一个性质：

甲：对于x∈R,都有f（1+x）=f（1－x）；　　

乙：在（－∞, 0）上函数递减；

丙：在（0,+∞）上函数递增；　　　　　　　

丁：f（0）不是函数的最小值.

如果其中恰有三个学生说得正确,请写出一个这样的函数：　 f（x）=x²－2x+1等.（开放型，答案不唯一）

三、解答题：74分

17．（12分)已知集合，集合，，求：（1）A∩B （2）

C_U（A∪B）

18．（12分）若集合，且，求实数的值。

解：由；因此，-----（1分）

（1）若时，得，此时，；　 -----（3分）

（2）若时，得，-------------------(4分)

若,满足------(5分)　 即 ， --(7分)

故所求实数的值为或或 --------------(8分)

19．本题共两小题，其中第一题5分，第二题7分：

（1）已知f(x)=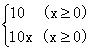求f[f(-7)]之值。

（2）已知f(x)＝3x²＋1，g(x)是一次函数且其图象过点（0，-1） （1，1），求f[g(x)]．

解：(1)、∵f(－7)＝10，∴f[f(－7)]＝f(10)＝100．

（2）、由已知得f[g(x)]＝3(2x－1)²＋1＝12x²－12x＋4

20．（12分）对于集合A，B，定义A×B={（a，b）a∈A，b∈B}.

①若A={1,2},B={3,4},求A×B；

②若A×B＝｛（１，２），（２，２）｝，求A，B；

③若A中有m个元素,B中有n个元素,则A×B中有几个元素?

【解析】①A×B＝{（1,3）,（1,4）,（2,3）,（2,4）}…………………………2分

②A={1,2},B={2}…………………………………………5分

③mn个……………………………………………………8分

21．（12分）小娟利用国庆放假在一服装店勤工俭学, 对某品牌服装一周的销售单价与日均销售量的关系记载如下:

销售单价/元	70	75	80	85	90	95
日均销售量/件	44	42	40	38	36	34

　 其中每件进价为40元(不计其他费用), 你能根据以上数据作出分析, 向小娟建议怎样的定价才能获得最大利润。(利润=销售总价进货总价).

解:根据表中所给数据可知:单价每增加5元, 销售量将减少2件 --------(1分)

　　 设定价为元, 则日均销售量为件　　　 --------(3分)

　　　-------- (5分)

　　　　 　　　　　　---------------- (7分)

. ----------------(8分)

22．（14分）已知二次函数的二次项系数为，且不等式的解集是，

　（1）若有两个相等的根，求的解析式

（2）若的最大值为正数，求的取值范围。

解：

（1）因为

所以

于是①

由方程　　  ②

因为方程②有两个相等的根，所以，

即　

由于代入①得的解析式

　 （2）由

及

由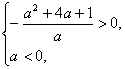 解得

故当的最大值为正数时，实数a的取值范围是

补：（12分）设x₁,x₂是关于x的一元二次方程x²－2(m－1)x＋m＋1=0的两个实根，又y=x²₁＋x²₂，

求y=f(m)的解析式及此函数的定义域.

解：∵x₁,x₂是x²－2(m－1)x＋m＋1=0的两个实根，

∴ =4（m－1）²－4(m＋1)0,解得m或m3。

又∵x₁＋x₂=2(m－1), x₁·x₂=m＋1,

∴y=f(m)=x₁²＋x₂²=(x₁＋x₂)²－2x₁x₂=4m²－10m＋2,

即y=f(m)=4m²－10m＋2(m0或m3)。