姓名______;_________班 高一数学立几阶段测试试题
数学测验试卷
___考室_____号 高一第一学期·必修二之立体几何阶段测试
一、选择题（共50分）
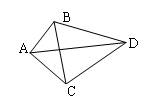★1．设A、B、C、D是空间四个不同的点，在下列命题中，不正确的是( )
（A）若AC与BD共面，则AD与BC共面
（B）若AC与BD是异面直线，则AD与BC是异面直线
(C) 若AB=AC，DB=DC，则AD=BC
(D) 若AB=AC，DB=DC，则AD 
BC
★2．已知正方体外接球的体积是
，那么正方体的棱长等于( )
A.2
B.
C.
D.
★3．过半径为2的球O表面上一点A作球O的截面，若OA与该截面所成的角是60°则该截面的面积是( )
A．π B. 2π C. 3π D. 
★4.设
、
是两条不同的直线，
、
是两个不同的平面.考查下列命题，其中正确的命题是（ ）A．
B．
C．
D．
★5.若
为一条直线，
为三个互不重合的平面，给出下面三个命题：
①
；②
；③
．其中正确的命题有（ ）
Ａ．0个 Ｂ．1个 Ｃ．2个 Ｄ．3个
★6.对于任意的直线l与平同a,在平面a内必有直线m,使m与l ( )
(A)平行 （B）相交 (C)垂直 (D)互为异面直线
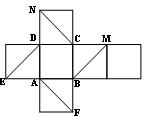
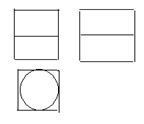
★7．如图是正方体平面展开图，在这个正方体中：①BM与ED平行；②CN与BE是异面直线；③CN与BM成60º角；④DM与BN垂直. 以上四个命题中，正确命题的序号是 （ ）
（A）
①②③ （B） ②④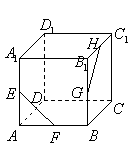 
（C）
③④ （D） ②③④
★8．如图，在正方体
中，
分别为
，
，
，
的中点，则异面直线
与
所成的角等于（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
★9．过平行六面体ABCD-A1B1C1D1任意两条棱的中点作直线,其中与平面DBB1D1平行的直线共有 ( )
A.4条 B.6条 C.8条 D.12条
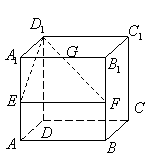★10、在棱长为1的正方体
中，
分别为棱
的中点，
为棱
上的一点，且
．则点到平面
的距离为（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
二、填空题（25分）
★11、已知某组合体的三视图如图所示，则该组合体是由______________组合而成的。
★12、一个长方体的各顶点均在同一球的球面上，且一个顶点上的三条棱的长分别为
，
，
，则此球的表面积为 ．
★13.设
是空间两条不同直线，
是两个不同平面，下面有四个命题：
①
②
③
④
其中真命题的编号是 （写出所有真命题的编号)
★14．已知平面
和直线，给出条件：①
；②
；③
；④
；⑤
.
（i）当满足条件
时，有
；（ii）当满足条件
___________时，有
.（填所选条件的序号）
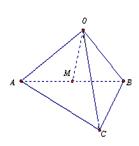
★15、在三棱锥
中，三条棱
、
、
两两互相垂直，且＝＝，
是边的中点，则
与平面
所成的角的大小是 _____________.（ 用反三角函数表示）；
三、解答题（75分）
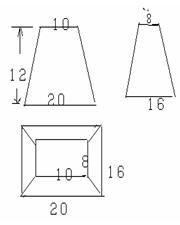
★16题、如图，是一个几何体的三视图，画出它的直观图，并求 出它的体积和表面积。
★
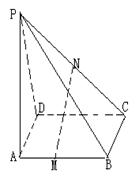17．如图，已知
是平行四边形
所在平面外一点，、
分别是、
的中点.
（1）求证：
平面
；
（2）若
，
， 求异面直线
与
所成的角的大小
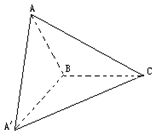
★18．三角形ABC中 AB=BC=1， ∠ABC=120o, 将三角形ABC所在平面沿BC边所在的直线旋转90 o之后，得到平面A′BC ，（1）求AA′与平面A′BC所成角的大小？（2）求二面角A-BA′-C的平面角的大小？（3）求点B到平面AA′C的距离？
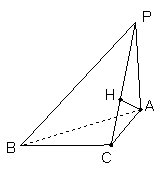
★19． 如图，已知△ABC中∠ABC=300，PA⊥平面ABC，PC⊥BC，PB与平面ABC所成角为450，AH⊥PC，垂足为H．
(1)求证：平面CAH⊥平面PBC；
(2)求二面角A—PB—C的大小．
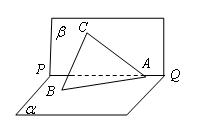★20．(2007湖南·文) 如图，已知直二面角
，
，
，
，
，
，直线
和平面
所成的角为
．（I）证明
；（II）求二面角
的大小．
★ 
21．(2007江西·文) 右图是一个直三棱柱（以
为底面）被一平面所截得到的几何体，截面为．已知
，
，
，
，
．（1）设点
是的中点，证明：
平面；（2）求与平面
所成的角的大小；（3）求此几何体的体积．
部分题答案
★1． C ★2． D ★3． ( A ) ★4. B ★5. C
★6. C ★7． C ★8． B ★9． D ★10、D
★11、组合体的三视图如图所示，则该组合体是由_圆柱和四棱柱_组合而成的。
★12、一长方体的各顶点均在同一球的球面上，且一个顶点上的三条棱的长分别为，，，则此球的表面积为
14π．
★13.是空间两条不同直线，是两个不同平面，下面有四个命题：
① ②
③
④
其中真命题的编号是 ①、④.;（写出所有真命题的编号)
★14．已知平面和直线，给出条件：①；②；③；④；⑤. （i）当满足条件 ③⑤时，有；（ii）当满足条件 ②⑤ 时，有.（填所选条件的序号）
★15、在三棱锥中，三条棱、、两两互相垂直，且＝＝，是边的中点，则与平面所成的角的大小是 
.（
用反三角函数表示）；
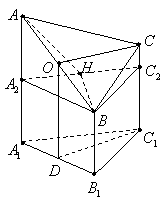★21．(2007江西·文) 右图是一个直三棱柱（以为底面）被一平面所截得到的几何体，截面为．已知，，，，．（1）设点是的中点，证明：平面；（2）求与平面所成的角的大小；（3）求此几何体的体积．
■（1）证明：作
交
于
，连
．
则
，因为是的中点，所以
．则
是平行四边形，因此有
，
平面
，且
平面；则面．（2）解：如图，过
作截面
面，分别交，
于
，
，作
于
，因为平面
平面，则
面．连结
，则
就是与面所成的角．因为
，
，所以
．与面所成的角为
．（3）因为，所以
．
．
．所求几何体的体积为
．