高一数学第一学期寒假作业1
班级 姓名 学号
1．左面的三视图所示的几何体是
2．下列命题：(1)平行于同一平面的两直线平行; (2)垂直于同一平面的两直线平行;
(3)平行于同一直线的两平面平行; (4)垂直于同一直线的两平面平行;
其中正确的有
3．设A在x轴上，它到P（0，
，3）的距离为到点Q（0，1，-1）的距离的两倍那么A点的坐标是
4．设Rt△ABC斜边AB上的高是CD，AC=BC=2, 沿高CD作折痕将之折成直二面
角A—CD—B（如图）那么得到二面角C—AB—D的余弦值等于
|
|
5．如图，
是体积为1的棱柱，则四棱锥
的体积是
6．根据表格中的数据，可以判定方程ex-x-2=0的一个根所在的区间为
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+2 | 1 | 2 | 3 | 4 | 5 |
7．点E，F，G，H分别为空间四边形ABCD中AB，BC，CD，AD
的中点， 若AC=BD，且AC与BD成900，则四边形EFGH是
|
8．已知定义在实数集上的偶函数
在区间（0，+
）上是增函数，那么
，
和
之间的大小关系为
9．直线y = x绕原点按逆时针方向旋转
后所得直线与圆 (x-2)2+y2=3的位置关系是
10．函数
在
上的最大值与最小值之和为
，则的值为
11．用一张圆弧长等于12
分米，半径是10分米的扇形胶片制作一个圆锥体模型，这个圆锥体的体积等于
立方分米。
12．直线l的斜率是-2，它在x轴与y轴上的截距之和是12，那么直线l的一般式方程是 。
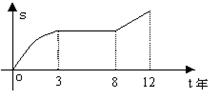13．某工厂12年来某产品总产量S与时间t(年)的函数关系如图所示，下列四种说法：
(1) 前三年总产量增长的速度越来越快；
(2) 前三年总产量增长的速度越来越慢；
(3) 第3年后至第8年这种产品停止生产了；
(4) 第8年后至第12年间总产量匀速增加。
其中正确的说法是 。 （第13题图）
14．把一坐标纸折叠一次，使得点(0，2)与（－2，0）重合，且点（2004，2005）与点（m，n）重合，则m－n的值为
15． 已知集合A=
，B={x2<x<10}，C={xx<a}，全集为实数集R.
(1) 求A∪B，(CRA)∩B；(2)如果A∩C≠φ，求a的取值范围。
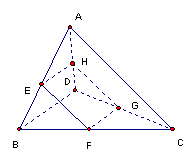
16、如图，长方体
中，
，
，点
为
的中点。
（1）求证：直线
∥平面
；
（2）求证：平面
平面
；
（3）求证：直线
平面。
17． 设实数
同时满足条件：
且
（1）求函数
的解析式和定义域；
（2）判断函数的奇偶性；
（3）若方程
恰有两个不同的实数根，求
的取值范围。
18
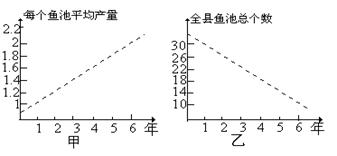．甲乙两人连续6年对某县农村鳗鱼养殖业的规模(总产量)进行调查,提供了两个方面的信息,分别得到甲、乙两图：
甲调查表明：每个鱼池平均产
量从第1年1万只鳗鱼上升到
第6年2万只。
乙调查表明：全县鱼池总个数
由第1年30个减少到第6年10个。
请你根据提供的信息说明：
（1）第2年全县鱼池的个数及全县出产的鳗鱼总数。
（2）到第6年这个县的鳗鱼养殖业的规模(即总产量)比第1年扩大了还是缩小了？说明理由。
（3）哪一年的规模(即总产量)最大?说明理由。
19． 圆
的半径为3，圆心在直线
上且在
轴下方，轴被圆截得的弦长为
。（1）求圆的方程；
（2）是否存在斜率为1的直线
，使得以被圆截得的弦
为直径的圆过原点？若存在，求出的方程；若不存在，说明理由。
楚水实验学校07-08学年第一学期高一数学寒假作业1参考答案
1. 六棱锥；2. (2)和(4)；3.（1，0，0）和（ -1，0，0）；4.
；
5. 
；6. (1,2)；7、正方形；8. y1 < y3 < y2 ；9、直线与圆相切；10. 
；
11．96 。 12、2x+y-8=0。 13 、(2) (3) (4)。 14、 -1 。
15． 解：（1）A∪B={x1≤x<10}-----------------------------------------（3分）
(CRA)∩B={xx<1或x≥7}∩{x2<x<10}---------------（6分）
={x7≤x<10}---------------------------------------（9分）
（2）当a>1时满足A∩C≠φ-----------------------（12分）
17解：（1）设AC和BD交于点O，连PO，
由P，O分别是，BD的中点，故PO//，所以直线∥平面--（4分）
（2）长方体中，，底面ABCD是正方形，则ACBD
又面ABCD，则AC，
所以AC面，则平面平面
-------------------------（9分）
（3）PC2=2，PB12=3，B1C2=5，所以△PB1C是直角三角形。PC，
同理PA，所以直线平面。--（14分）
19． 解：（1）
.------------------------- （1分）
又
------------------------- （2分）
.
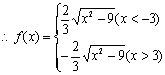函数的定义域为集合D=
.----------- （4分）
（2）当
有
，
=
--（6分）
同理，当
时，有
.
任设
,有
为定义域上的奇函数. ----------- （8分）
(3) 联立方程组
可得,
--------------------------（9分）
(Ⅰ)当
时,即
时,方程只有唯一解,与题意不符; 
-------- （10分）
(Ⅱ)当
时,即方程为一个一元二次方程,要使方程有两个相异实数根,则
解之得 
,但由于函数
的图象在第二、四象限。-----------（13分）
故直线的斜率
综上可知
或
------------------ （14分）
18． 解：由题意可知,图甲图象经过（1,1）和（6,2）两点,
从而求得其解析式为y甲=0.2x+0.8-----------------------（2分）
图乙图象经过（1,30）和（6,10）两点,从而求得其解析式为y乙=-4x+34.----- -- （4分）
(1)当x=2时，y甲=0.2×2+0.8 =1.2,y乙= -4×2+34=26，
y甲·y乙=1.2×26=31.2.
所以第2年鱼池有26个,全县出产的鳗鱼总数为31.2万只.------------ ---（6分）
(2)第1年出产鱼1×30=30（万只）, 第6年出产鱼2×10=20（万只）,可见,第6年这个县的鳗鱼养殖业规划比第1年缩小了----------------------------------（8分）
(3)设当第m年时的规模总出产量为n,
那么n=y甲·y乙=（0.2m+0.8） (-4m+34)= -0. 8m2+3.6m+27.2
=-0.8(m2-4.5m-34)=-0.8(m-2.25)2+31.25---------------------------（11分）
因此, .当m=2时,n最大值=31.2.
即当第2年时,鳗鱼养殖业的规模最大,最大产量为31.2万只. --------------（14分）
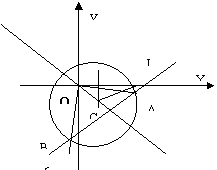20．
|
圆C的方程是（X-1）2+（Y+2）2=9--（4分）
（2）设L的方程y=x+b，以AB为直径的圆过原点，则
OAOB，设A（x1，y1），B（x2，y2），则
x1x2+ y1y2=0 ①---------------（6分）
由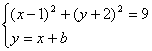
得
----------（8分）
要使方程有两个相异实根，则
△=
＞0 即
<b<
---------（9分）
------------------------------------------（10分）
由y1=x1+b，y2=x2+b，代入x1x2+ y1y2=0，得2x1x2+（x1+x2）b+b2=0---------（12分）
即有b2+3b-4=0，b=-4,b=1（舍去） -----------------------------------------------（13分）
故存在直线L满足条件，且方程为
或
----------------------（14分）