高一数学第一学期寒假作业3
班级 姓名 学号
1. 若U={1,2,3,4},M={1,2}, N={2,3}, 则CU(M∪N)=
2、下列根式中,分数指数幂的互化,正确的是
(1)![]() (2).
(2).![]() (3).
(3).![]() (4).
(4).![]()
3.函数![]() 的定义域为
的定义域为
4、若A(-2,3),B(3,-2),C(![]() ,m)三点共线,则m的值为
,m)三点共线,则m的值为
5、以A(1,3)和B(-5,1)为端点线段AB的中垂线方程是
6、方程![]() 表示一个圆,则m的取值范围是
表示一个圆,则m的取值范围是
7、圆![]() 上的点到直线
上的点到直线![]() 的距离的最大值是
的距离的最大值是
8、直线过点P(0,2),且截圆![]() 所得的弦长为2,则直线的斜率为
所得的弦长为2,则直线的斜率为
9、 直线![]() :
:![]() 与曲线
与曲线![]() :
:![]() 有两个公共点,则
有两个公共点,则![]() 的取值范围是
的取值范围是
10、函数![]() ,当
,当![]() 时是增函数,则
时是增函数,则![]() 的取值范围是
的取值范围是
11.一个正四棱柱的侧面展开图是一个边长为4的正方形,则它的体积为___________.
12、已知A(-2,3,4),在y轴上求一点B,使![]() ,则点B的坐标为
。
,则点B的坐标为
。
13、已知集合A =![]() ,B=
,B=![]() ,A∩B={3,7},
,A∩B={3,7},
求![]() 。
。
14.已知函数![]() (1)判断
(1)判断![]() 的奇偶性;
的奇偶性;
(2)判断并用定义证明![]() 在
在![]() 上的单调性。
上的单调性。
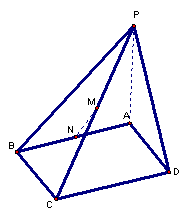
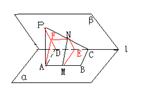
15、如图: PA⊥矩形ABCD所在平面,M,N分别是AB,PC的中点。
(1)求证:M N∥平面PAD。
(2) 求证:M N⊥CD。
(3) 若∠PDA=45°,求证; MN⊥平面PCD.
16、(本题12分)已知圆的方程为![]() 求圆的过P点的切线方程以及切线长。
求圆的过P点的切线方程以及切线长。
17、求过直线![]() 和
和![]() 的交点,且垂直于直线
的交点,且垂直于直线![]() 的直线方程。
的直线方程。
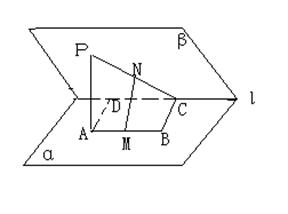
18、如图:在二面角![]() 中,A、B
中,A、B![]() ,C、D
,C、D![]() ,ABCD为矩形,
,ABCD为矩形,![]() 且PA=AD,M、N依次是AB、PC的中点,
且PA=AD,M、N依次是AB、PC的中点,
(1)求二面角![]() 的大小
的大小
(2)求证:![]()
(1) 求异面直线PA和MN所成角的大小
![]()
![]()
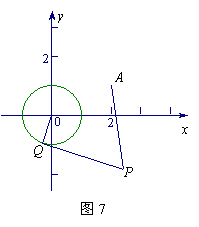
 19、已知⊙O:
19、已知⊙O:![]() 和定点A(2,1),由⊙⊙O外一点
和定点A(2,1),由⊙⊙O外一点![]() 向⊙⊙O引切线PQ,切点为Q,
向⊙⊙O引切线PQ,切点为Q,
且满足![]() .
.
(1) 求实数a、b间满足的等量关系;
(2) 求线段PQ长的最小值;
(3) 若以P为圆心所作的⊙P与⊙O有公共点,试求半径取最小值时⊙P的方程.
楚水实验学校07-08学年第一学期高一数学寒假作业3参考答案
1、 {4};2、(3);3、![]() ;4、
;4、![]() ;5、3x+y+4=0; 6、 m<
;5、3x+y+4=0; 6、 m< ![]() ;7.
;7.![]() ;
;
8、![]() ;9.
;9. ![]() ; 10、
; 10、![]() ; 11、 4; 12、(0,8,0)
或 (0,-2 ,0)
; 11、 4; 12、(0,8,0)
或 (0,-2 ,0)
13、a=1 0,1,2,3,7
14、解:(1)![]() 的定义域为
的定义域为![]() ,且
,且![]()
所以,![]() 为
为![]() 上的奇函数。
上的奇函数。
(2)设对于任意的![]() ,由于
,由于
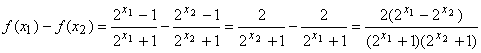
又 ![]() ,所以
,所以![]() 。故
。故 ![]() 在
在![]() 上单调递增的。
上单调递增的。
15、取PD中点E, 连接AE, ME 以下略
16(1)若切线的斜率存在,可设切线的方程为![]() 即
即![]()
则圆心到切线的距离![]() 解得
解得![]() 故切线的方程为
故切线的方程为![]()
(2)若切线的斜率不存在,切线方程为x=2 ,此时直线也与圆相切。
综上所述,过P点的切线的方程为![]() 和x=2.
和x=2.
![]() 17:解方程组
得
17:解方程组
得 ![]() 所以交点坐标为
所以交点坐标为![]()
又因为直线斜率为K=![]() , 所以求得直线方程为27x+54y+37=0
, 所以求得直线方程为27x+54y+37=0
18:解:(1)连结PD∵ABCD为矩形∴AD⊥DC, 即
又PA⊥![]() ,∴PD⊥
,∴PD⊥![]() ,∴
,∴![]() PAD为二面角
PAD为二面角![]() 的平面角,又∵PA⊥AD,PA=AD
的平面角,又∵PA⊥AD,PA=AD
∴![]() PAD是等腰直角三角形,∴
PAD是等腰直角三角形,∴![]() PDA=450,即二面角
PDA=450,即二面角![]() 的平面角为450。
的平面角为450。
(2)证明:过M作ME∥AD,交CD于E,连结NE,则ME⊥CD,
NE⊥CD,∴CD⊥平面MNE, MN⊥CD,又∵AB∥CD,MN⊥AB。
(3)解:过N作NF∥CD,交PD于F,∵ N是PC的中点
∴F是PD的中 点,连结AF,可以证明四边形AMNF是平行四边形
∴AF∥MN,![]() PAF是异面直线PA和MN所成的角,∵ PA=PD, ∴F是PD的中点,∴AF是
PAF是异面直线PA和MN所成的角,∵ PA=PD, ∴F是PD的中点,∴AF是![]() PAD的平分线,∵
PAD的平分线,∵ ![]() PAD=900 ∴
PAD=900 ∴![]() PAF=450,∴异面直线PA和MN所成的角为450。
PAF=450,∴异面直线PA和MN所成的角为450。
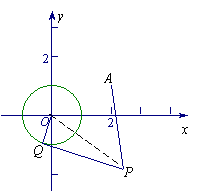 19、解:(1)连
19、解:(1)连![]()
![]() 为切点,
为切点,![]() ,由勾股定理有
,由勾股定理有
![]() .
.
又由已知![]() ,故
,故![]() .
.
即:![]() .
.
化简得实数a、b间满足的等量关系为:![]() .
.
(2)由![]() ,得
,得![]() .
.
![]()
![]() =
=![]() .
.
故当![]() 时,
时,![]() 即线段PQ长的最小值为
即线段PQ长的最小值为![]()
解法2:由(1)知,点P在直线l:2x + y-3 = 0 上.
∴ PQ min = PA min ,即求点A 到直线 l 的距离.
∴ PQ min = = .
(3)设![]() P 的半径为
P 的半径为![]() ,
,
![]()
![]() P与
P与![]() O有公共点,
O有公共点,![]() O的半径为1,
O的半径为1,
![]() 即
即![]() 且
且![]() .
.
而![]() ,
,
故当![]() 时,
时,![]() 此时,
此时, ![]() ,
,![]() .
.
得半径取最小值时![]() P的方程为
P的方程为![]() .
.
解法2: ![]() P与
P与![]() O有公共点,
O有公共点,![]() P半径最小时为与
P半径最小时为与![]() O外切(取小者)的情形,而这些半径的最小值为圆心O到直线l的距离减去1,圆心P为过原点与l垂直的直线l’ 与l的交点P0.
O外切(取小者)的情形,而这些半径的最小值为圆心O到直线l的距离减去1,圆心P为过原点与l垂直的直线l’ 与l的交点P0.
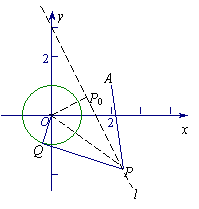 r = -1 = -1.
r = -1 = -1.
又 l’:x-2y = 0,
解方程组![]() ,得
,得![]() .即P0( ,).
.即P0( ,).
∴ 所求圆方程为![]() .
.