高一数学第一学期寒假作业4
班级 姓名 学号
 1.下列几何体中是旋转体的有
;
1.下列几何体中是旋转体的有
;
①圆柱;②六棱锥;③正方体;④球体;⑤四面体.
2.如图,平面![]() 、
、![]() 、
、![]() 可将空间分成 ;
可将空间分成 ;
3.直线x – y +7= 0的倾斜角等于
4.如果直线 a x + 2y+2=0 与直线3x – y–2=0平行, 那么a等于
5.下列结论中, 正确的有
⑴ 垂直于同一条直线的两条直线平行. ⑵ 垂直于同一条直线的两个平面平行.
⑶ 垂直于同一个平面的两条直线平行. ⑷ 垂直于同一个平面的两个平面平行.
6.正方体的内切球的体积为![]() , 则此正方体的表面积是
, 则此正方体的表面积是
 7.若方程
7.若方程![]() 表示圆,则
表示圆,则![]() 的取值范围是
的取值范围是
8.圆![]() 关于直线
关于直线![]() 对称的圆的方程是
对称的圆的方程是
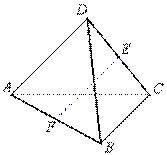
9.如图,三棱锥![]() 中,
中,![]() ,且
,且![]() ,
,![]() 分别
分别
是棱![]() 的中点,则
的中点,则![]() 和
和![]() 所成的角等于
所成的角等于
10.经过原点的直线![]() 与圆
与圆![]() 有公共点, 则直线
有公共点, 则直线![]() 的斜率的取值范围是
的斜率的取值范围是
|
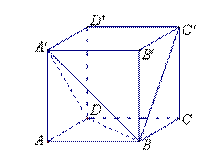 11.如图,三棱柱
11.如图,三棱柱![]() 的所有棱长都相等,侧棱与底面垂直,
的所有棱长都相等,侧棱与底面垂直,![]() 是侧棱
是侧棱![]() 的中点, 则二面角
的中点, 则二面角![]() 的大小为
的大小为
 |
第11题图 第12题图
12.在正方体![]() 中,直线
中,直线![]() 与平面
与平面![]() 所成的角的余弦值等于
所成的角的余弦值等于

13.请写出所给三视图表示的简单组合体由哪些几何体组成.
.
14.经过圆![]() 的圆心,并且与直线
的圆心,并且与直线
![]() 垂直的直线方程为______
.
垂直的直线方程为______
.
15.已知实数![]() 满足
满足![]() ,则
,则![]() 的最小值为________.
的最小值为________.
16.已知点![]() 与两个定点
与两个定点![]() ,
,![]() 的距离的比为
的距离的比为![]() ,则点
,则点![]() 的轨迹方程为_______
.
的轨迹方程为_______
.
17.过点![]() 的直线
的直线![]() 与
与![]() 轴的正半轴、
轴的正半轴、![]() 轴的正半轴分别交于点
轴的正半轴分别交于点![]() 、
、![]() ,
,![]() 为坐标原点,
为坐标原点,![]() 的面积等于6,求直线
的面积等于6,求直线![]() 的方程.
的方程.
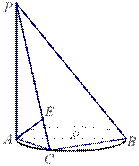 18.如图,
18.如图,![]() 垂直于⊙
垂直于⊙![]() 所在的平面,
所在的平面,![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 是⊙
是⊙![]() 上一点,过点
上一点,过点![]() 作
作![]() ,垂足为
,垂足为![]() . 求证:
. 求证:![]() 平面
平面![]()
|
19.如图,四棱锥![]() 中,四边形
中,四边形![]() 是平行四边形,
是平行四边形,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点. 求证:
的中点. 求证:![]() 平面
平面![]() .
.

20.一圆与![]() 轴相切,圆心在直线
轴相切,圆心在直线![]() 上,且被直线
上,且被直线![]() 截得的弦长为
截得的弦长为![]() ,求此圆的方程.
,求此圆的方程.
21.已知圆![]() 与圆
与圆![]()
(其中![]() ) 相外切,且直线
) 相外切,且直线![]() 与圆
与圆![]() 相切,求
相切,求![]() 的值.
的值.
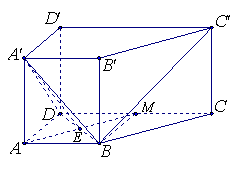
22.如图,四棱柱![]() 中,侧棱与底面垂直,
中,侧棱与底面垂直,![]() ,
,![]() ,且
,且![]()
![]()
![]()
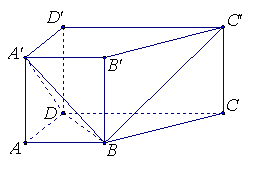 (1)求证:
(1)求证:![]() ;
;
(2)求二面角![]() 的大小.
的大小.
楚水实验学校07-08学年第一学期高一数学寒假作业4答案
1、①和④;2、六部分;3、![]() ;4、
;4、![]() ; 5、⑵
⑶;6、216;
; 5、⑵
⑶;6、216;
7. ![]() ;8.
;8. ![]() ;9.
;9.![]() ;
;
10. (![]() ,
,![]() )∪[
)∪[![]() ,+
,+![]() ]; 11.
]; 11. ![]() ; 12.
; 12.![]()
13.由圆柱和圆锥组成 ;14.![]() ;15. 5 ;16.
;15. 5 ;16.![]()
17.解:设直线![]() 的方程为
的方程为![]() ,则
,则![]() ,
,![]() ,由已知得
,由已知得![]() ,且
,且![]() .
.
因为 ![]() 的面积等于6,所以
的面积等于6,所以 ![]() ,所以
,所以![]() .…………3分
.…………3分
因为点![]() 在直线
在直线![]() 上,所以
上,所以![]() ,所以
,所以 ![]() ,
,![]() ,
,
代入![]() ,得
,得![]() ,所以
,所以![]() ,解得
,解得![]() . ……6分
. ……6分
所以![]() ,直线
,直线![]() 的方程为
的方程为![]() ,即
,即![]() …………8分
…………8分
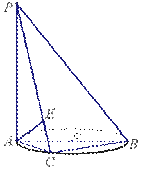 18.证明:因为
18.证明:因为 ![]() 平面
平面![]() 所以
所以 ![]()
又因为 ![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 是⊙
是⊙![]() 上一点,
上一点,
所以 ![]() 所以
所以 ![]() 平面
平面![]() …………5分
…………5分
而![]() 平面
平面![]() 所以
所以 ![]()
又因为 ![]() ,所以
,所以 ![]() 平面
平面![]() …………8分
…………8分
19.证明:取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() .…………1分
.…………1分
因为 ![]() ,
,![]() ,
,
 所以
所以 ![]() ,且
,且![]() ………3分
………3分
又因为 四边形![]() 是平行四边形,且
是平行四边形,且![]() 是
是![]() 的中点.
的中点.
所以 ![]() ,且
,且![]() ………5分
………5分
所以 ![]()
![]()
![]() ,所以
四边形
,所以
四边形![]() 是平行四边形,
是平行四边形,
所以 ![]() .
.
又因为 ![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以 ![]() 平面
平面![]() .…………………………………………10分
.…………………………………………10分
注意:此题也可以取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,可以利用平面与平面平行的判定定理证明 平面
,可以利用平面与平面平行的判定定理证明 平面![]() 平面
平面![]() ,从而得出
,从而得出![]() 平面
平面![]() .
.
20.解:设圆的方程为![]() ,由已知得
,由已知得
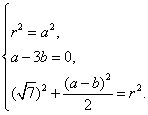 解得
解得![]() 或
或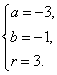 ……………9分
……………9分
故所求圆的方程为![]() 或
或![]() …………10分
…………10分
21.解:由已知,![]() ,圆
,圆![]() 的半径
的半径![]() ;
;![]() ,圆
,圆![]() 的半径
的半径![]() .
.
因为 圆![]() 与圆
与圆![]() 相外切,所以
相外切,所以 ![]() .…………4分
.…………4分
整理,得![]() . 又因为
. 又因为 ![]() ,所以
,所以 ![]() .……………6分
.……………6分
因为直线![]() 与圆
与圆![]() 相切,所以
相切,所以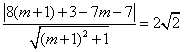 ,
,
即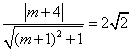 .……………………8分
.……………………8分
两边平方后,整理得![]() ,所以
,所以![]() 或
或![]() .…………………………10分
.…………………………10分
22.解:(1)作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.
 因为
因为 ![]() ,
,![]() ,
,![]() ,
,
且![]()
所以 四边形![]() 是正方形,
是正方形,
所以 ![]() 所以
所以 ![]() .
.
又因为 ![]() 所以
所以 ![]() ,
,
所以 ![]() ,所以
,所以 ![]() ,所以
,所以 ![]() .……3分
.……3分
又因为 ![]() 平面
平面![]() ,所以
,所以 ![]() .…………………4分
.…………………4分
(2)设![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() . 由(1)知,
. 由(1)知,![]() ,且
,且![]() .
.
因为 ![]() 平面
平面![]() ,所以
,所以 ![]() ,
,![]()
又因为 ![]() 所以
所以 ![]() .又因为
.又因为 ![]() ,所以
,所以 ![]()
综上可知![]() 是二面角
是二面角![]() 的平面角. ……………7分
的平面角. ……………7分
在![]() 中,因为
中,因为 ![]() ,
,![]() ,
,
所以 ![]() ,所以
,所以 ![]() ,所以
,所以 ![]() ,
,
所以 二面角![]() 的大小为
的大小为![]() .…………………………10分
.…………………………10分
注意:本题的第(1)问也可以通过计算得出![]() ,
,![]() ,
,![]() ,
,
所以 ![]() ,因此,
,因此,![]()