高一数学第一学期期中三校联考
高一数学试卷
命题人：余小静 审核人：方红兵
考生须知：
1、 本卷满分100分，考试时间90分钟。
2、 答题前，在答题卷密封区内填写学校、班级、姓名和考号。
3、 所有答案必须写在答题卷上，写在试题卷上无效
4、 考试结束，只需上交答题卷
一、 选择题：本大题共10小题，每小题3分，共30分。在每小题中只有一项是符合题目要求的。
1、若集合A={1，3，x}，B={1，
}，A∪B={1，3，x}，则满足条件的实数x的个数有（ ）
（A） 4个 （B） 3个 （C）2个 （D） 1个
2、幂函数
的图象过点
，那么
的值为
（ ）
(A )
(B) 64 (C) 
(D) 
3、设偶函数f（x）的定义域为R，当
时f（x）是增函数，则
的大小关系是（ ）
（A）
＞
＞
（B）＞＞
（C）＜＜ （D）＜＜
4、已知函数
，其中n
N，则f（8）=（
）
（A）2 （B）4 （C） 6 （D）7
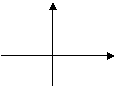
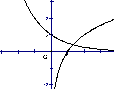
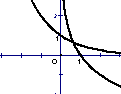
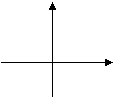
5、设
则在同一坐标系中函数
的图像是( )
 | |||
| |||
 | |||
 | |||
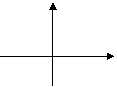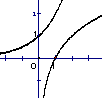
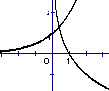
(A) (B) (C) (D)
6、将函数
的图像向左平移一个单位长度，再向上平移3个单位长度，就可以得到（ ）的图象
(A) 
(B)
(C)
(D) 
7、如果函数在区间
上是递增的，那么实数
的取值范围是( )
(A) a≤－3 (B) a≥－3 (C) a≤5 (D) a≥5
8、今有一组实验数据如下：
| t | 1.99 | 3.0 | 4.0 | 5.1 | 6.12 |
| v | 1.5 | 4.04 | 7.5 | 12 | 18.01 |
现准备用下列函数中的一个近似地表示这些数据满足的规律，其中最接近的一个是：
(A) 
(B) 
(C) 
(D) 
9、函数y=
的单调递增区间（ ）
(A)（
） (B)（
） (C) [-2，-1] (D) [-5，-2]
10、方程
的解所在区间是 ( )
(A) (0,2) (B) (1,2) (C) (2,3) (D) (3,4)
二、填空题：本大题有5小题，每小题4分，共20分。请将答案填写在答题卷中的横线上。
11、 已知集合
，其真子集的个数为 ▲
12、已知定义在R上的奇函数，当
时，
，那么当
时，
▲ ; 当
时， ▲ .
13、若
，则
▲
14、函数
在
上的最大值与最小值的和是 ▲
15、给定的函数
，有下列4个命题：①对于任意
均有
；
② 
；③ 在
上是增函数；④ 
有最小值0.
其中正确命题的序号是 ▲ （请将所有正确命题的序号都填上）.
三、解答题：本大题有5小题，共50分。解答应写出文字说明，证明过程或演算步骤。
16、计算下列各式（本小题满分8分）
（Ⅰ）
（Ⅱ） 
17.（本小题满分10分）
已知集合
（1）求
；
（2）若
，求的取值范围。
18、(本题满分10分)
已知
为偶函数
（1）
求
的值
（2）
用定义证明：函数在
上是增函数
19、（本小题满分10分）
纳税是每个公民应尽的义务，从事经营活动的有关部门必须向政府税务部门交纳一定的营业税。某地区税务部门对餐饮业的征收标准如下表
| 每月的营业额 | 征税情况 |
| 1000元以下（包括1000元） | 300元 |
| 超过1000元 | 1000元以下（包括1000元）部分征收300元， 超过部分的税率为4% |
（1）写出每月征收的税金y（元）与营业额x（元）之间的函数关系式，并画出函数图象
（2）某饭店5月份的纳税额为500元，则这个月该饭店的营业额是多少？？
20.（本题满分12分）
已知函数定义在
上，对于任意的
，有
，且当时，
；
（1）验证函数
是否满足这些条件；
（2）判断这样的函数是否具有奇偶性和其单调性，并加以证明；
（3）若
，试解方程