高一数学第一学期期中检测试卷
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。共150分，考试时间120分钟。
第Ⅰ卷（选择题共60分）
一：选择题：本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的.选项填涂在答题卡上。
1、设集合
，则
＝（ ）
A、
B、
C、
D、
2、 满足条件
的集合
的个数是
A、4 B、3 C、2 D、1
3. 不等式（x＋1）（2－x）＞0的解集为
A、
B、
C、
D、
4、“p或q为真命题”是“p且q为真命题”的
A、充分不必要条件
B、必要不充分条件
C、充要条件 D、既不充分也不必要
5、下列各组函数中，表示同一函数的是
A 、
B、
C 、
D、
6、函数
的定义域为[4，7]，则
的定义域为
A、（1，4） B [1，2]
C、
D、 
7．若函数
在区间
上是减函数，则实数
的取值范围是
A、
B、
C、
D、
8、已知
的图象恒过（1，1）点，则
的图象恒过
A．（－3，1） B．（5，1） C．（1，－3） D．（1，5）
9、已知
，则
A. 
B.
C.
D.
10、若函数
在
上有最小值
，则实数a的值为
A、－２ Ｂ、２ Ｃ、０或
Ｄ、－
11. 方程x2-6x
=a有不同的四个解，则a的范围是
A、a
9
B、0a9
C、0<a<9 D、0<a9
12、已知集合A={a，b，c}，B={1，2，3，4，5，6}。f：A
是从A到B的映射，则满足f(a)>f(b)=f(c)的映射个数为
A、10 B、15 C、20 D、21
第Ⅱ卷（非选择题共90分 ）
二、填空题：本大题共4小题，每小题4分，共16分，把答案填在答题纸上。
13、设集合
，集合
，若
，则
_____；
14、某商人将彩电先按原价提高40%，然后“八折优惠”，结果是每台彩电比原价多赚144元，那么每台彩电原价是 元．
15、函数
的定义域_________________;
16、命题“若a、b是偶数，则a+b是偶数”的逆否命题是____________________________;
三、解答题：本大题共6小题，共74分，解答题应写出文字说明，证明过程或演算步骤，在答题纸上相应题目的答题区域内作答.
17、（本小题满分12分）
解下列不等式：（1）
（2）
18.（本小题满分12分）
已知M={x -2≤x≤5}, N={x a+1≤x≤2a-1}.
（Ⅰ）若M
N，求实数a的取值范围；（Ⅱ）若M
N，求实数a的取值范围.
19、（本小题满分12分）
利用单调函数的定义证明：函数
上是减函数.
20、（本小题满分12分）
已知集合
只有一个元素，
，
。（1） 求
（2）设N是由可取的所有值组成的集合，试判断N与的关系。
21、一动点P从边长为1的正方形ABCD的一个顶点A出发，沿着正方形的边界运动一周最后回到点A，若点P运动的路程为x，点P到点A的距离为y，求y与x的函数关系式，并指出函数的定义域和值域。
22、已知二次函数f(x) = ax2+bx+c（a≠0）满足条件对称轴方程为x=1，f(2)=0，且方程f(x)=x有等根．
（1）求a、b、c的值；
（2）是否存在实数m，n(m<n)，使得函数f(x)在定义域 [m，n] 上的值域为[3m，3n]．如果存在，求出m，n的值；如果不存在，请说明理由．
容城中学2007——2008学年度第一学期期中检测
高一数学试卷
13题 ____________ 14题 __
15题 16题 ________________
17.解：
高一数学试卷答案
一、DCDBC DABBA CB
二、13、
14、1200 15、
。
16、-1
三、17（1）
……………………………………… 3
不等式的解集为
………………………………5
(2)
…….6
①
…………………………………………………....8
②
…………………………………………….10
③
…………………………………………..12
18. 解：（Ⅰ）由于MN，则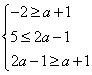
，解得a∈Φ…………………………….4
（Ⅱ）①当N=Φ时，即a＋1＞2a－1，有a＜2…………………………………….…….4
②当N≠Φ，则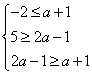
，解得2≤a≤3，.
综合①②得a的取值范围为a≤3……………………………………………………4
19、.证明：设
是区间
上的任意两个实数，且
…………… 1分
则 
……………………………………………
4分
…………………………………………………….. 6分
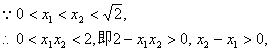
………………………………. 8分
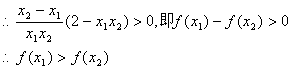
………………….10分
由单调函数的定义可知，函数上是减函数…………….12分
20（1）由
得
，则
由
得
，则
………………..3分
………………………………6分
（2） 因为集合M只有一个元素，则
当
时，方程
只有一个实数解，符合题意；
当
时，
解得
……………………………….10分
则 
…………………………………………12分
21、设动点P按A-B-C-D-A的顺序沿正方形的边界运动一周，则
当
时，距离
当
时， 
，
当
时， 
当
时， 
。
………………………………………………8分
所求函数关系式是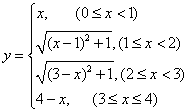
，……………………………10分
函数的定义域为
，值域为
…………………………………….12分
22、（1）图象的对称轴方程为x=1．
…………………………………2
方程f(x)=x有等根．
……………………………….4
解得a = 
，b=1，c=0．…………………………………………………….6
（2）f(x)
= 
=
≤
……………………………..8
m＜n≤
Þf(x)在[m，n]上为增函数
Þf(m) = 3m，f(n) = 3n………………………………………………………………12
Þm = -4，n=0（m=0，n = -4，不合，舍去）．…………………………..14
…………