高一数学第二学期期中考试卷

高一数学第二学期期中考试卷

班级：　　　　　 考号：　　　　　　　  姓名；　　　　　　　　 总分：

1．本试卷分第Ⅰ卷共150分．考试时间120 分钟．

2．请将各题答案填在试卷答题卷上．

一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中．只有一项是符合题目要求的．

1.下列给出的赋值语句中正确的是（　 ）

A．  B． C．　 D．

2　将两个数交换,使,下面语句正确一组是 (　　)

a=c c=b b=a

b=a a=b

c=b b=a a=c

a=b b=a

　A　　　　　　　 B　　　　　　　　　C　　　　　　　　　 D　 

3.某公司甲、乙、丙、丁四个地区分别有150 个、120个、180个、150个销售点．公司为了调查产品销售的情况，需从这600个销售点中抽取一个容量为100的样本，记这项调查为①；在丙地区中有20个特大型销售点，要从中抽取7个调查其收入和售后服务等情况，记这项调查为②．则完成①、②这两项调查宜采用的抽样方法依次是（　）.

A．分层抽样法，系统抽样法　　　　　　　　　 B．分层抽样法，简单随机抽样法

C．系统抽样法，分层抽样法　　 　　　　D．简单随机抽样法，分层抽样法

4.一个袋中装有1个红球和1个白球，现从袋中取出1球，然后放回袋中再取出一球，则取出的两个球同色的概率是（　 ）

A. 　　　　B. 　　　C. 　　　 D.　

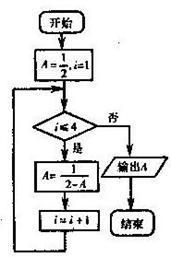
5．如图所示的程序框图输出的结果是　　　　  （　　）

A．　 B．

C．　　 D．

6. 已知地铁列车每10 min一班，在车站停1 min.

则乘客到达站台立即乘上车的概率是　　　　　　　　　　　　 　　（　 ）

A.　　  B.　　 C.　　D.

7．当时，下面的程序段结果是 (　　)

A　　　B　　　C　　　D　

8．根据一组数据判断是否线性相关时，应选用（　　）

　　　A．散点图　 　　　　　　　　　　　　　　　　　 B．茎叶图　　

　　　C．频率分布直方图　　　　　　　　　　　　　　D．频率分布折线图

9．甲乙两人下棋，甲获胜的概率为30％，甲不输的概率为70％，

则甲乙两人下一盘棋，最可能出现的情况是 （　 ）

A．甲获胜　 B．乙获胜　　C．二人和棋 　D．无法判断

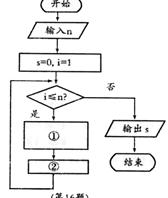
10. 下面为一个求20个数的平均数的程序,在横线上应填充的语句为 (　　)

	S=0 i=1 DO  INPUT　x  S=S+x  i=i+1 LOOP UNTIL　_____ a=S/20 PRINT　a END

A.  i>20

 B.  i<20

C.  i>=20

D.　　　　 i<=20

11．从2008名学生中选取50名学生参加数学竞赛，若采用下面的方法选取：先用简单随机抽样从2008人中剔除8人，剩下的2000人再按系统抽样的方法抽取50人，则在2008

人中，每人入选的概率　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A． 不全相等　　　　　　　　　　　　　　　　　　　　　B．均不相等

　　　 C．都相等，且为　　　　　　　　　　　　　 D．都相等，且为

12. 甲、乙两支女子曲棍球队在去年的国际联赛中，甲队平均每场进球数为3.2，全年比赛进球个数的标准差为3；乙队平均每场进球数为1.8，全年比赛进球个数的标准差为0.3.下列说法正确的个数为①甲队的技术比乙队好　②乙队发挥比甲队稳定　③乙队几乎每场都进球　④甲队的表现时好时坏（　 ）

A.1　　　　  B.2　　　　　 C.3　　　　　 D.4

二、填空题：本大题共4小题，每小题6分，共24分，把答案填在答题卷中的横线上

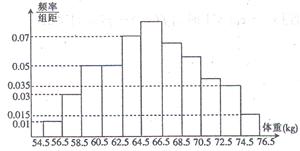13．为了了解某地区高三学生的身体发育情况，

抽查了该地区100名年龄为17岁-18岁

的男生体重（kg），得到频率分布直方

图如下图所示。据图可得这100名学

生中体重在 的学生人数

是　　　　　　 。

14．右图为甲、乙两名篮球运动员每场比赛的得分情况的茎叶图，则甲运动员的得分的中位数是___________；

乙运动员的得分的中位数是___________

甲、乙两名乙运动员发挥更稳定的是___________

15．二进制数转换成十进制数是_______三个数的最大公约数是________。

16．右图给出的是计算的值的一个程序框图（其中n的值由键盘输入），其中①处应填　　　　　　  ，②处应填　　　　　　　　

三、解答题：解答应写出必要的文字说明、证明过程及演算步骤．

17（12分）用秦九韶算法计算多项式当x=2时的值。

分组	频数	频率
[12.45,12.95）
[12.95,13.45）
[13.45,13.95）
[13.95,14.45）
合计	10	1.0

2.4.6

18．（13分）有同一型号的汽车100辆,为了解这种汽车每蚝油1L所行路程的情况,现从中随即抽出10辆在同一条件下进行蚝油1L所行路程实验,得到如下样本数据（单位:km）:13.7,12.7,14.4,13.8,13.3,12.5,13.5,13.6,13.1,13.4，其分组如下:

（1）完成上面频率分布表；

（2）根据上表,在给定坐标系中画出频率分布直线图,并根据样本估计总体数据落在

[12.95,13.95]中的概率；

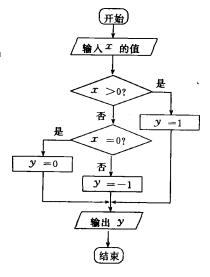19．（12分）已知函数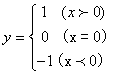及框图 ，编程序。　　　　　　　　  　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

20（13分）．甲乙两人约定5：00到6：00在图书馆见面，甲只愿意等10分钟，乙愿意等20分钟，则他们见到的概率有多大？

21. （12分） 某种产品的广告费支出x与销售额y(单位：百万元)之间有如下的对应数据：

（1）请画出上表数据的散点图；

（2）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程y=x+；

x	2	4	5	6	8
y	30	40	50	60	70

（3）要使这种产品的销售额突破一亿元(含一亿元)，则广告费支出至少为多少百万元？（精确到0.1）. 参考公式：，.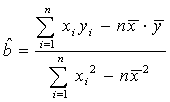

（22）、（本小题满分14分）小明、小华用4张扑克牌（分别是黑桃2、黑桃4，红桃5、红桃6）玩游戏，他们将扑克牌洗匀后，背面朝上放在桌面上，小明先抽，小华后抽，抽出的牌不放回，各抽一张。

（1）若小明恰好抽到黑桃4；

①请列出各种可能出现的情况； ②求小华抽出的牌的牌面数字比4大的概率。

（2）求小明、小华至少有一人抽到的牌是黑桃的概率

（3）小明、小华约定：若俩人有人抽到黑桃牌且小明抽到的牌的牌面数字比小华的大，则小明胜，反之，则小明负，你认为这个游戏是否公平，说明你的理由。