第一学期
高一数学必修1结业考试试题
一、选择题：（每小题5分，共12个小题）。每个小题只有一个答案符合题意。
1． 将集合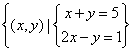
表示成列举法，正确的是：（ B ）
A、{2，3} B、{（2，3）} C、{x=2，y=3} D、（2，3）
2．下列各组函数中，表示同一个函数的是：（ D ）
A、y=x-1和
B、y=x0和y=1
C、f(x)=x2 和g(x)=(x+1)2
D、
和
3、若x>y>1，0<a<1，那么正确的结论是（ D ）
A、ax>ay B、ax>1 C、a-x<1 D、a-x>a-y
4、函数
的零点所在的大致区间是（ B ）
A、（1，2） B、（2，3） C、（e，3） D、（e，+∞）
5．函数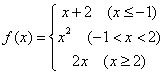
，若f(x)=3，则x的值是：（ D
）
A、1 B、
C、
或1 D、
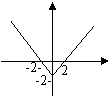
6、设函数y=f(x)的图像如图所示，则f(x)的解析式为（ A ）
A、y=x-2 B、y=x-2
C、y=-x+2 D、y=x+2
7、下列结论正确的是：（ B ）
A、偶函数的图象一定与y轴相交
B、奇函数y=f(x)在x=0处有意义，则f(0)=0
C、定义域为R的增函数一定是奇函数
D、图象过原点的单调函数一定是奇函数
8、设a>0且a≠1，函数f(x)=loga(2x-1)+1的图象恒过定点P，则P的坐标是（ A ）
A、（1，1） B、（-1，1） C、（1，-1） D、（-1，-1）
9、若关于x的方程2x-1+2x2+a=0有两实数解，则a的取值范围是（ B ）
A、
B、
C、
D、
10、 函数y=elnx-x-1的图象大致是（ D ）
11、若0<a<1，且f(x)=logax，则下列各式中成立的是（ D ）
A、f(2)>f(1/3)>f(1/4) B、f(1/4)>f(2)>f(1/3)
C、f(1/3)> f(2)>f(1/4) D、f(1/4)> f(1/3)>f(2)
12、设函数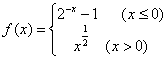
,若f(x0)>1，则x0的取值范围是（ D ）
A、（-1，1） B、（-1，+∞） C、（-∞，-2） D、（-∞，-1）∪（1，+∞）
二、填空题：（每小题5分，共4个小题。）将正确答案填写在题中的横线上。
13、已知映射f：N→N*
，x→x2+1，则f(x)=0的原象是_____3______。
14、已知f(x)的定义域为
，则函数f(x2)的定义域为______
__________。
15、如果二次函数f(x)=x2-(a-1)x+5在区间上是增函数，那么a的取值范围是
_a≤2__.
16、给出下列函数：
① 函数y=ax与函数y=logaax(a>0且a≠1)的定义域相同。
② y=x3与y=3x的值域相同。
③ 函数
与
均是奇函数。
④ 函数y=(x-1)2与y=2x-1在R+上都是增函数。
其中正确命题的序号是__①③__。
三、解答题：（共6个小题）要求写出解题的主要过程。
17、已知全集U={1，2，3，4，5，6，7，8}，A={x1≤x≤5，x∈Z}，B={x2<x<9,x∈Z}。
（1） 求A∩B;
（2） 求（CUA）∪(CUB)。（10分）
解：（1）A∩B={3，4，5}
（2）（CUA）∪(CUB)= CU（A∩B）={1，2，6，7，8}
18、设函数f(x)=x2-2x-3
(1)求函数f(x)的零点；
（2）画出函数图像，并写出单调区间。
解：（1）f(x)=x2-2x-3=0，x=3或x=-1 ∴函数f(x)的零点为x=3或x=-1；
（2）对称轴：x=1 单增区间：[-1，1]，
单减区间：，[1，3]
19、已知函数
（a为常数）
（1） 证明：函数f(x)在(-∞,+∞)上是减函数；
（2） 若f(x)为奇函数，求a的值。（12分）
（1）证明：在(-∞,+∞)上任取两个点x1，x2且x1＜x2
f(x1)-f(x2)= (
)-(
)
=
-
=
∵2>1且x1＜x2 ∴
>0而
∴f(x1)-f(x2)>0即f(x1)>f(x2) ∴函数f(x)在(-∞,+∞)上是减函数。
（2）∵f(x)为奇函数且在x=0处有意义，∴f(0)=0
∴
∴
20 、某旅游公司有客房300间，每间房租为200元，每天客满，公司欲提高档次，并提高租金。如果每间客房每日增加20元，客房出租就减少10间，若不考虑其他因素，公司将房租提高到多少时，每天客房的租金总收入最高？（10分）
解：设公司将房租提高x个20元，则每天客房的租金收入y为：
y=(200+20x)(300-10x) （x∈N）
=60000+4000x-200x2
这个二次函数图像的对称轴为：
200+20x=200+20×10=400
当x=10时，y最大值=80000.
答：将房租提高到400元/间时，客房的租金总收入最高，每天为80000元。
21、已知函数
在区间
上为增函数，求a的取值范围。（12分）
解：令g(x)=x2-ax-a
∵f(x)=logag(x)在上为增函数，∴g(x)应在上为减函数
且g(x)>0在上恒成立
因此：
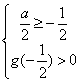即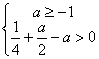
解得：
故实数a的取值范围是：
22、已知函数f(x)=ax2+(2a-1)x-3 (a≠0)在区间[-3/2，2]上的最大值为1，求实数a的值。（14分）
解：二次函数f(x) =ax2+(2a-1)x-3
(a≠0)的对称轴为
①若x=-3/2时函数取最大值，则
解得：a=-10/3
此时函数的对称轴为x=-23/20，所以在区间[-3/2，2]上当x=-23/20时函数取最大值。所以a=-10/3不符合题意。
②若x=2时函数取最大值，则a×22+(2a-1)×2-3=1, 解得：a=3/4
此时函数的对称轴为x=-1/3，所以在区间[-3/2，2]上当x=2时函数取最大值。
所以a=3/4符合题意。
③若时函数取最大值，则
解得：
(没打完)