高一数学必修2练习题（一）
1.1空间几何体的结构，1.2空间几何体的三视图和直观图，1.3空间几何体的表面积和体积
A组题（共100分）
一．选择题：本大题共5题，每小题7分，共35分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1．在棱柱中（ ）
A．只有两个面平行 B．所有的棱都平行
C．所有的面都是平行四边形 D．两底面平行，且各侧棱也互相平行
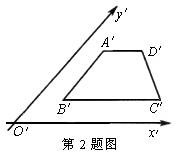
2．如图中直观图所示的平面图形是（ ）
A．任意四边形 B．直角梯形
C．任意梯形 D．等腰梯形
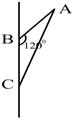
3．矩形ABCD中，AB＝5厘米，AD＝2厘米，以直线AB为轴旋转一周，所得圆柱的侧面积为（ ）
A．20π平方厘米 B．28π平方厘米
 |
C．50π平方厘米 D．70π平方厘米
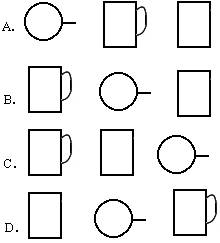
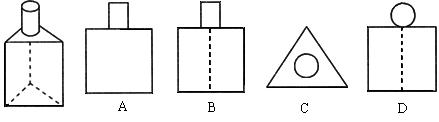
4．如图所示茶杯，其正视图、侧视图及俯视图依次为（ ）
5．一个球的外切正方体的表面积的等于6cm2，则此球的体积为（ ）
A．
B．
C．
D．
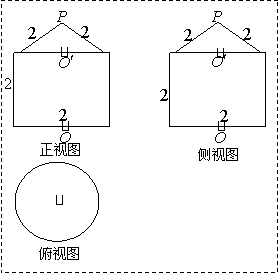
二．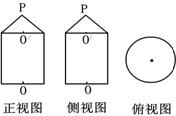
填空题：本大题共4小题，每小题6分，共24分。
6．右图所示为一简单组合体的三视图，它的上部是一个__________下部是一个_________.
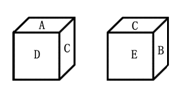7．一个正方体的六个面上分别有字母
，如下图所示是此正方体的两种不同放置，则与D面相对的面上的字母是_________.
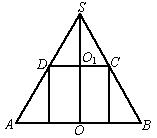
8．圆锥的高是10 cm，侧面展开图是半圆，此圆锥的侧面积是_____；轴截面等腰三角形的顶角为______．
9．将4×6的矩形铁皮作为圆柱的侧面卷成一个圆柱，则圆柱的最大体积是_______．
三．解答题：本大题共3小题，共41分，解答题应写出文字说明、证明过程或演算步骤。
10．在一个直径为
的圆柱形水桶中将一个球全部放入水里，水面升高
.求这个球的表面积.
11、如图．已知几何体的三视图（单位：cm）．
（Ⅰ）画出它的直观图（不要求写画法）；
（Ⅱ）求这个几何体的表面积和体积．
12．用刀切一个近似球体的西瓜，切下的较小部分的圆面直径为30 cm，高度为5 cm，该西瓜体积大约有多大?
B组题（共100分）
四．选择题：本大题共5题，每小题7分，共35分。在每小题给出的四个选项中，只有一项是符合题目要求的。
13．如图一个封闭的立方体，它6个表面各标出1、2、3、4、5、6这6个数字，现放成下面3个不同的位置，则数字l、2、3对面的数字是（ ）
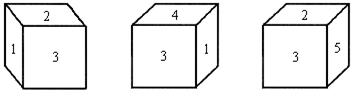
A．4、5、6 B．6、4、5 C．5、4、6 D．5、6、4
14．已知正方体、球、底面直径与母线相等的圆柱，它们的表面积相等，则它们的体积的大小关系是（ ）
A．V正方体
V圆柱V球
B．V正方体
V圆柱V球
C．V正方体
V圆柱V球
D．V圆柱V正方体V球
|
，
，
，如图所示。若将△ABC绕
旋转一周，则所形成的旋转体的体积是（ ）
（A）
（B）
（C）
（D）
16．如图，下列选项不是几何体的三种视图为（ ）
17．已知正四面体ABCD的表面积为S，其四个面的中心分别为E、F、G、H，设四面体EFGH的表面积为T，则
等于（ ）
A．
B．
C．
D．
五．填空题：本大题共4小题，每小题6分，共24分。
18．半径为1的球的内接正方体的体积是________；外切正方体的体积是_______．
19．已知一平面图形的斜二测直观图是底角等于45°，上底和腰均为1的等腰梯形，则原图形的面积为________．
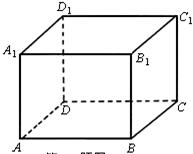
20．如图，长方体ABCD—A1BlClD1中，AD＝3，AAl＝4，AB＝5，则从A点沿表面到Cl的最短距离为______．
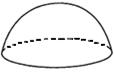
21．如图所示，桌上放着一个半球，则在它的三视图及从右面看到的图中，有三个图相同，一个不同，这个不同的图应该是_________．
六．解答题：本大题共3小题，共41分，解答题应写出文字说明、证明过程或演算步骤。
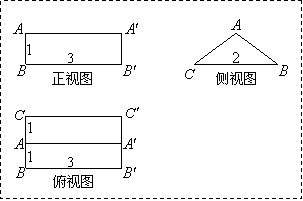
22．如图1－1是一个几何体的三视图（单位：cm）
（Ⅰ）画出这个几何体的直观图（不要求写画法）；
（Ⅱ）求这个几何体的表面积及体积；
（Ⅲ）设异面直线
与
所成的角为
，求
．
23．一个无盖的正方体盒子展开后的平面图如图所示，A、B、C是展开图上的三点，则在正方体盒子中，∠ABC的度数是多少?
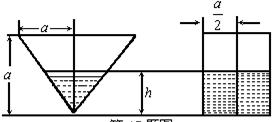
24．一个圆锥形容器和一个圆柱形容器，它们的轴截面尺寸如图所示，两容器内所盛液体的体积正好相等，且液面高度h正好相同，求h．
C组题（共50分）
七．选择或填空题：本大题共2题。
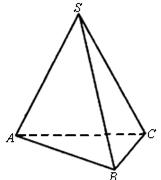
25．在三棱锥S—ABC中，SA＝SB＝SC＝1，∠ASB＝∠ASC＝∠BSC＝30°，如图，一只蚂蚁从点A出发沿三棱锥的表面爬行一周后又回到A点，则蚂蚁爬过的最短路程为_____．
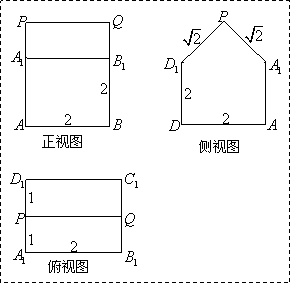
26．由小正方体木块搭成的几何体的三视图如下图，则该几何体由_________块小正方体木块搭成．
正视图 侧视图 俯视图
八．解答题：本大题共2小题，解答题应写出文字说明、证明过程或演算步骤。
27．如图，已知几何体的三视图（单位：cm）．
（Ⅰ）画出这个几何体的直观图（不要求写画法）；
（Ⅱ）求这个几何体的表面积及体积；
（Ⅲ）设异面直线
、
所成角为，求．
28．圆锥的底面半径为5 cm，高为12 cm，当它的内接圆柱的底面半径为何值时，圆锥的内接圆柱全面积有最大值？最大值是多少?
厦门市2007—2008学年数学必修2练习（一）参考答案
A组题（共100分）
1、D 2、B 3、A 4、C 5、C
6、圆锥 圆柱 7、B 8、
；60°
9、
10、
11、解（Ⅰ）这个几何体的直观图如图2－2所示．
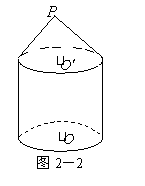（Ⅱ）这个几何体是一个简单组合体，它的下部是一个圆柱（底面半径为1cm，高为2cm），它的上部是一个圆锥（底面半径为1cm，母线长为2cm，高为
cm）．
所以所求表面积
，
所求体积
．
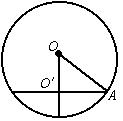
12、解：如图，设球半径为Rcm，切下的较小部分圆面半径为15cm，∴OO′＝R－5．
Rt△OO′A中，R2－（R－5）2＝15，
∴R=25（cm）．
V＝
＝
＝
（cm3）．
B组题（共100分）
13、C 14、B 15、D 16、A 17、A
18、
；8 19、2＋
20、
21、俯视图
22、解：（Ⅰ）这个几何体的直观图如图1－2所示．
（Ⅱ）这个几何体是直三棱柱．
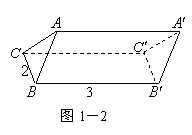由于底面
的高为1，所以
．
故所求全面积
．
这个几何体的体积
（Ⅲ）因为
，所以与所成的角是
．
在
中，
，
故
．
23、解：由平面图得直观图，如图所示，显然有AB＝AC＝BC，所以∠ABC＝60°．
24、设圆锥形容器的液面的半径为R，则液体的体积为
πR2h，圆柱形容器内的液体体积为π（
）2h．
根据题意，有πR2h＝π（）2h，解得R＝
．
再根据圆锥轴截面与内盛液体轴截面是相似三角形，得
＝
，所以h＝．
C组题（共100分）
25、 26、7、
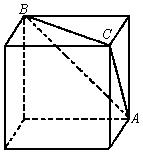
27、解：（Ⅰ）这个几何体的直观图如图2－4所示．
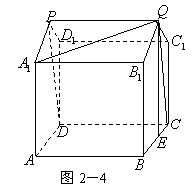（Ⅱ）这个几何体可看成是由正方体
及直三棱柱
的组合体．
由
，
，
可得
．
故所求几何体的全面积
所求几何体的体积
（Ⅲ）由
，且
，可知
，
故
为异面直线、所成的角（或其补角）．
由题设知
，
，
取中点
，则
，且
，
．
由余弦定理，得
．
28、如图SAB是圆锥的轴截面，其中SO＝12，OB＝5．设圆锥内接圆柱底面半径为O1C＝x，由△SO1C∽△SOB，
则
＝
，SO1＝·O1C＝
，
∴OO1＝SO－SO1＝12－，则圆柱的全面积S＝S侧＋2S底＝2π（12－）x＋2πx2＝2π（12x－
）．
当x＝
cm时，S取到最大值
cm2．
