高一数学必修2练习题（二）
2.1空间点、直线、平面之间的位置关系，2.2直线、平面平行的判定及其性质
A组题（共100分）
一、选择题：本大题共5题，每小题7分，共35分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1．有四个命题：
a)
直线
在平面
内，直线
在平面
内，且
相交，则平面与重合
b)
直线共面，直线
相交，则直线
共面。
c)
直线在平面内，
与平行，则与面没有公共点
d) 有三个公共点的两个平面一定重合
以上命题中错误命题的个数是（ ）
（A）1个（B）2个（C）3个（D）4个
2、已知
，则
等于（ ）
A 
B 
C 
D 以上几个都不对
3、如果直线
直线b，且a//平面，那么b与的位置关系是（ ）
A
相交 B 
C 
D 
4、下列语句中，正确的个数为 （ ）
（1）一条直线和另一条直线平行，它和经过另一条直线的任何平面平行
（2）一条直线和一个平面平行，它和这个平面内的任何直线平行
（3）过平面外一点和这个平面平行的直线只有一条
（4）平行于同一个平面的两条直线互相平行
A 0 B 1 C 2 D 3
5、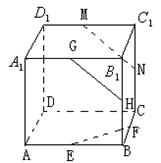
如右图，ABCD--
是正方体，
分别为所在棱的中点，则下列结论正确的是（ ）
和
为平行直线，和
为相交直线
和为平行直线，和为相交直线
和为相交直线，和为异面直线
和为异面直线，和也是异面直线
二、填空题：本大题共4小题，每小题6分，共24分。
6、已知是两条异面直线，a上有三个点，b上有两个点，这些点可确定 个平面
7．不共线的三个平面两两相交，可将空间分成 个部分．
8、在正方体
的六个表面中，与
异面组成
角的对角线共有
条。
9、长方体ABCD--中，已知三条棱
，
，
，则异面直线与
所成的角的度数为
三、解答题：本大题共3小题，共41分，解答题应写出文字说明、证明过程或演算步骤。
10．已知在正方体
中，E、F分别是
的中点，
求证：平面
平面
11、已知E、F、G、M分别是四面体的棱AD、CD、BD、BC的中点，
求证：AM
面EFG
12、如图，四边形ABCD是矩形，
面ABCD，过BC作平面BCFE交AP于E，
|
|
|
|
|
|
|
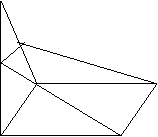交DP于F，求证：四边形BCFE是梯形
B组题（共100分）
四、选择题：本大题共5题，每小题7分，共35分。在每小题给出的四个选项中，只有一项是符合题目要求的。
13．A,b是异面直线，A ,B是a上的两点，C, D是b上的两点，M ,N分别是线段AC,BD的中点，则MN和a的位置关系为（ ）
A 异面 B平行 C相交 D以上三种关系都有可能
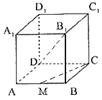
14．如图所示，在正方体
中，M为AB的中点，则异面直线
与CM所成角的余弦值为（ ）
(A)
(B)
©
(D)
15、已知直线与直线垂直，平行于平面，则与平面的位置关系是（ ）
A．
B．
C．与平面相交 D．以上都有可能
16、
是空间四边形，
分别是四条边
的任意四点，则下列结论正确的是（ ）
A.
和
是相交直线 B. EH和FG是平行直线
C. 
和
是异面直线 D. 以上情况都有可能
17、正方体中，
、
、
分别是
、
、
的中点．那么正方体的过、、的截面图形是（ ）
A．三角形 B．四边形 C．五边形 D．六边形
五、填空题：本大题共4小题，每小题6分，共24分。
18．三个平面将空间最少分成
部分，最多分成
部分，则
等于
．
19．三条直线中有两条平行，第三条和这两条都相交时确定 个平面；三条直线交于一点时可确定 个平面；三条直线互相平行时，最多可确定 个平面。
20．连接抛物线上任意四点组成的四边形可能是
（填写所有正确选项的序号）
①菱形 ②有3条边相等的四边形 ③梯形
④平行四边形 ⑤有一组对角相等的四边形
21．已知m、n是不同的直线，
是不重合的平面，给出下列命题：
①若
则
②若
则
③m、n是两条异面直线，若
则
上面命题中，真命题的序号是____________(写出所有真命题的序号)
六、解答题：本大题共3小题，共41分，解答题应写出文字说明、证明过程或演算步骤。
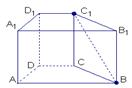
22．正方体ABCD—A1B1C1D1
的棱长为
⑴求△AB1D1的面积；⑵求三棱锥
的体积。
 |
23．已知直四棱柱
中，
，底面
是直角梯形，
，
，
，
，
，求异面直线
与
所成的角的余弦值
24、过正方体的棱
作一平面交平面
于
，
求证：//
C组题（共50分）
七、选择或填空题：本大题共2题。
25、平面
平面
，平面
平面
，平面
平面
，若
，
则
与的位置关系是（ ）
A．与异面
B．与相交
C．至少与中的一条相交 D．与都平行
26．平面过直线
外的两点，若要这个平面与平行，则这样的平面有 （ ）
A 无数个 B 一个 C不存在 D上述情况都有可能
八、解答题：本大题共2小题，解答题应写出文字说明、证明过程或演算步骤。
27．如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的，其中AB=4，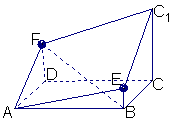
BC=2，CC1=3，BE=1求BF的长；
28．两个全等的正方形ABCD和ABEF所在平面相交于AB，M∈AC，N∈FB，且AM=FN，求证：MN∥平面BCE。
厦门市2007—2008学年数学必修2练习（二）参考答案
1、C 2、B 3、D 4、A 5、B
6、5 7、7 8、8 9、60
10、提示：
，取的中点H，连接EH，
，有
所以四边形
是平行四边形，所以
，又
，
所以
11、,提示：连结MD交GF于H，则点H为MD的中点
12、分析：因为
，所以BC//面ADP，所以BC//EF，所以EF//AD，但EF的长度
小于
的长度，而
，所以EF的长度小于BC的长度
13、A 14、D 15、D 16、D 17、D
18、11 19、1，1或3，3 20、（2），（3），（5） 21、（3）
22、（1）易证△
为等边三角形，其边长等于2，所以△的面积为
。
（2）三棱锥的体积为
23、由题意AB∥CD,
∴∠C1BA是异面直线BC1与DC 所成的角或其补角.
连结AC1与AC,在Rt△ADC中,可得AC=
.又在Rt△ACC1中,可得AC1=3.
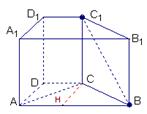在梯形ABCD中,过C作CH∥AD交AB于H,得∠CHB=90°,CH=2,HB=3, ∴CB=
.
又在Rt△CBC1中,可得BC1=
,
在△ABC1中,由余弦定理可得cos∠C1BA=
24、分析：因为//
面，所以//面
25．D 26、D
27、过E作EH//BC交CC1于H，则CH=BE=1，EH//AD，且EH=AD.
又∵AF∥EC1，∴∠FAD=∠C1EH.
∴Rt△ADF≌Rt△EHC1. ∴DF=C1H=2.
28、法一：分别过M、N作MM1⊥BC，NN1⊥BE，M1、N1为垂足。辅助平面由MM1与NN1构造，M1N1为辅助平面MM1N1N与平面BCE的交线，下证MN∥M1N1。
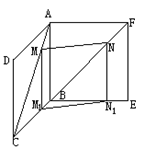∵ MM1∥AB
∴ 
①
∵ NN1∥EF
∴ 
②
∵ AC=BF，AM=FN
∴ CM=BN
又AB=EF
∴ 由①②得MM1=NN1
∴ MM1N1N为平行四边形
∴ MN∥M1N1
∴ MN∥平面BCE
法二；利用面面平行的性质
此时，同样要在MN基础上构造与平面BCE平行的辅助平面
过M、N分别作AB的垂线，设垂足分别为M2、N2
∵ MM2∥CB
∴ 
∵ NN2∥AF
∴ 
∵ AM=FN，AC=FB
∴ AM2=AN2
∴ M2与N2重合
∴ 平面MM2N∥平面BCE
∴ MN∥平面BCE