高一数学必修2练习题（三）
3.1直线的倾斜角与斜率 3.2直线的方程 3.3直线的交点坐标与距离公式
A组题（共100分）
一．选择题：本大题共有5小题，每小题7分，共35分．在每小题给出的四个选项中，有且只有一项是符合题目要求的。
1、过点(1，3)，斜率为1的直线方程是
（A）x－y＋2=0 （B）x－y－2＝0
（C）x＋y－4＝0 （D）x＋y－2=0
2、如果直线
与直线
平行，则
的值为
（A）3 （B）－3 （C）5 （D）0
3、过点P（4，－1）且与直线3x－4y＋6＝0垂直的直线方程是（ ）
（A）4x＋3y－13＝0 （B）4x－3y－19＝0
（C）3x－4y－16＝0 （D）3x＋4y－8＝0
4、在坐标平面上，不等式组
所表示的平面区域面积为
A．
B．
C．
D．2
5、到直线
的距离为2的直线方程是.
A. 
B.
或
C. D.
或 
二．填空题：本大题共有4小题，每小题6分，共24分．把答案直接填在答题卷相应题的横线上．
6、直线l在y轴上截距为2，且与直线l`：x+3y-2=0垂直，则l的方程是
7、非负实数x、y满足
的最大值为
.
8、两直线
与x轴相交且能构成三角形，则m满足的条件是
9、已知点
和
则过点
且与
的距离相等的直线方程为
.
三．解答题：本大题共3小题，共40分．解答应写出文字说明，证明过程或演算步骤．
10、（本小题满分13分）
已知直线l经过直线5x－2y＋3＝0和5x＋y－9＝0的交点，且与直线2x＋3y＋5＝0平行，求直线l方程.
11、（本小题满分14分）
已知直线
与直线
没有公共点，
求实数m的值
12、（本小题满分14分）
已知：两点A
，B（3，2），过点P（2，1）的直线l与线段AB有公共点求直线l的倾斜角的取值范围。
B组题（共100分）
一．选择题：本大题共有5小题，每小题7分，共35分．在每小题给出的四个选项中，有且只有一项是符合题目要求的。
1、若l1与l2为两条不重合的直线，它们的倾斜角分别为
，
，斜率分别为k1，k2，则下列命题
（1）若l1∥l2，则斜率k1=k2； （2）若斜率k1=k2，则l1∥l2；
（3）若l1∥l2，则倾斜角=；（4）若倾斜角=，则l1∥l2；
其中正确命题的个数是
A、1 B、2 C、3 D、4
2、光线由点P（2，3）射到直线
上，反射后过点Q（1，1），则反射光线所在的直线方程为
A、
B、
C、
D、
3、已知直线
与
互相垂直，垂足为（1，c）,则
的值为
A、－4 B、20 C、0 D、24
4、若点A（2，–3），B（–3，–2），直线
过点P（1，1），且与线段AB相交，则的斜率
的取值范围是
A．
或
B．或
C．
D．
5、设集合
，则A所表示的平面区域(不含边界的阴影部分)是
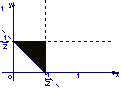
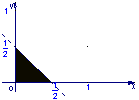
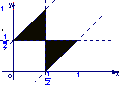
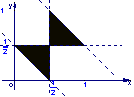
A． B． C． D．
二．填空题：本大题共有4小题，每小题6分，共24分．把答案直接填在答题卷相应题的横线上．
6、 经过点P（－3，—4），且在x轴、y轴上的截距相等的直线L的方程是
7、过点（－2，1），倾斜角的正弦为
的直线方程为 .
8、直线
关于直线
对称的直线方程是__________.
9、一条光线经过点P（–2，3）射到
轴上，反射后经过点Q（1，1），入射光线所在的直线的方程是
，反射光线所在的直线的方程是
.
三．解答题：本大题共3小题，共41分．解答应写出文字说明，证明过程或演算步骤．
10、（本小题满分13分）
已知直线被两平行直线
所截得的线段长为3，且直线过点（1，0），求直线的方程.
11、（本小题满分14分）
已知两点A（2，3）、B（4，1），直线l：x+2y－2=0，在直线l上求一点P.
（1）使PA+PB最小；
（2）使PA－PB最大.
12、（本小题满分14分）
为了绿化城市，准备在如图所示的区域内修建一个矩形PQRC的草坪，且PQ∥BC,RQ⊥BC,另外△AEF的内部有一文物保护区不能占用，经测量 AB=100m,BC=80m,AE=30m,AF=20m．
(1) 求直线EF的方程．
(2) 应如何设计才能使草坪的占地面积最大？
C组题（共50分）
一．填空题：把答案直接填在答题卷相应题的横线上．
1、设实数x, y满足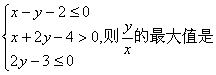
.
2. 已知两直线a1x+b1y+1=0和a2x+b2y+1=0的交点为P（2，3），过两点Q1（a1，b1）、Q2（a2，b2）（a1≠a2）的直线方程是 .
二．解答题：
3、已知长方形的四个顶点A（0，0）、B（2，0）、C（2，1）和D（0，1），一质点从AB的中点P0沿与AB夹角为θ的方向射到BC上的点P1后，依次反射到CD、DA和AB上的点P2、P3和P4（入射角等于反射角）.设P4的坐标为（x4，0）.若1<x4<2，求tanθ的取值范围.
4、设实数x、y满足不等式组
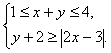
（1）求点(x,y)所在的平面区域；
（2）设
，在（1）所求的区域内，求函数
的最值
答案与提示
A组：
| 题号 | 1 | 2 | 3 | 4 | 5 |
| 答案 | A | B | A | B | B |
6. 3x – y +2 = 0 7. 9 8.. m≠ 0且m≠ -3 9. x+4y-7=0或x=-1
10.解：先求两直线的交点，联立方程组
得，
.
∵ 直线l与直线2x＋3y＋5＝0平行，
∴ 可设直线l的方程为：2x＋3y＋b＝0， 将x＝1，y＝4代入得b＝－14，
故所求直线l的方程为：2x＋3y－14＝0.
11.解：由题意可知：当m≠0时
≠
, m－２≠0 ,;解得:m=3,m=－1,m≠±3,m≠2
当m=0时两直线分别为x+6=0, －2x=0 即 x=－6, x=0 两直线没有公共点
综合以上知:当m=－1,或m=0时两直线没有公共点.
∴m的取值为－1
12. 解:当l与线段AB有公共点时，其倾斜角最小为直线PB的倾斜角α，
最大为直线PA的倾斜角为β，
∵直线AP的斜率为KAP=
∴α=1500
∵直线BP的斜率为KBP=
∴β=450
∴直线l的倾斜角θ的取值范围为：450≤θ≤1500
B组：
| 题号 | 1 | 2 | 3 | 4 | 5 |
| 答案 | D | C | A | A | A |
6. 4x-3y=0或x+y+7=0
7. 
8. 
9. 
；
10.y=0或3x-4y-3=0.
11.解：（1）可判断A、B在直线l的同侧，设A点关于l的对称点A1的坐标为（x1，y1）.
|
+2·
－2=0，
·（－）=－1.
|
x1=－
，
y1=－
.
由两点式求得直线A1B的方程为y=
（x－4）+1，直线A1B与l的交点可求得为P（
，－
）.由平面几何知识可知PA+PB最小.
（2）由两点式求得直线AB的方程为y－1=－（x－4），即x+y－5=0.
直线AB与l的交点可求得为P（8，－3），它使PA－PB最大.
12.解：（1）如图，在线段EF上任取一点Q，分别向BC,CD作垂线．
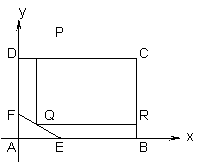由题意，直线EF的方程为：+=1
（2）设Q（x,20-x）,则长方形的面积
S=（100-x）[80-（20-x）] (0≤x≤30)
化简，得 S= -x2+x+6000 (0≤x≤30)
配方，易得x=5,y=时，S最大，其最大值为6017m2
C组：
1. 2. 2x+3y+1=0.
3.解：设P1B=x，∠P1P0B=θ，则CP1=1－x，∠P1P2C、∠P3P2D、∠AP4P3均为θ，
∴tanθ=
=x.又tanθ=
=
=x， ∴CP2=
=
－1.
而tanθ=
=
=
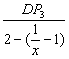=x，∴DP3=x（3－）=3x－1.
又tanθ=
=
=
=x，∴AP4=
=
－3.
依题设1<AP4<2，即1<－3<2， ∴4<<5，
>
>
.
∴>tanθ>.
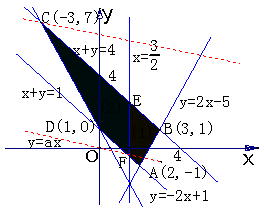4.解：（1）已知的不等式组等价于
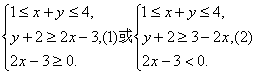
解得点
所在的平面区域为所示的阴影部分（含边界）
其中，
（2）表示直线
在y轴上的截距，且直线与（1）中所求区域有公共点
∵,
∴当直线过顶点C时，最大
∵C点的坐标为（-3，7），
∴的最大值为
如果-1＜≤2，那么当直线过顶点A（2，-1）时，最小，最小值为-1-2.如果＞2，那么当直线过顶点B（3，1）时，最小，最小值为1-3