等比数列单元测试
(时量60分钟)
班次 姓名
一.选择填空题
1.等比数列
中，
，则的前4项和为
（
B ）
A． 81 B． 120 C．168 D． 192
2在各项都为正数的等比数列｛an｝中，首项a1=3 ，前三项和为21，则a3+ a4+ a5=(C )
( A ) 33 ( B ) 72 ( C ) 84 ( D )189
3.设等比数列
的前n项和为Sn，若
，则
（ C
）
A．1:2 B．2:3 C．3:4 D．1:3
4. 已知Sn是等比数列
等于 （ A
）
A．
B．－ C．
D．－
5. 在
和
之间插入三个数，使这五个数成等比数列，则插入的三个数的乘积为_______216 __．
二. 已知各项均为正数的等差数列{an}，其前n项和Sn满足10Sn＝an2＋5an＋6；等比数列{bn}满足b1＝a1，b2＝a3，b3＝a15,求数列{bn}的通项公式；
解∵10Sn＝an2＋5an＋6， ① ∴10a1＝a12＋5a1＋6．
解之，得a1＝2，或a1＝3．……………………………………………………………2分
又10Sn－1＝an－12＋5an－1＋6（n≥2）， ②
由①－②，得 10an＝（an2－an－12）＋6（an－an－1），即（an＋an－1）（an－an－1－5）＝0．
∵an＋an－1＞0，∴an－an－1＝5（n≥2）．…………………………………………………5分
当a1＝3时，a3＝13，a15＝73．a1， a3，a15不成等比数列，∴a1≠3．
当a1＝2时，a3＝12，a15＝72，有 a32＝a1a15．…………………………………………7分
∴数列{bn}是以6为公比，2为首项的等比数列，bn＝2×6n－1． ………………………9分
三.已知数列
是等差数列，
是等比数列，且
,
,
(I)
求数列的通项公式；
(II)
求数列的通项公式.
解（I）
是等比数列，且
，
……………………………………3分
……………………6分
（II）数列
是等差数列，，
又
……………………………………10分
………………12分
题23.已知数列{an}的各项均为正数，Sn为其前n项和，对于任意
，满足关系
.
（Ⅰ）证明：{an}是等比数列；
（Ⅱ）在正数数列{cn}中，设
，求数列{lncn}中的最大项.
（Ⅰ）证明：∵
①
∴
② …………2分
②－①，得
∵
故数列{an}是等比数列 ………………5分
（Ⅱ）解：据（Ⅰ）可知 
由，得
…………8分
令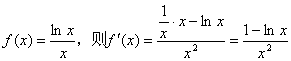
∵在区间（0，e）上，
∴在区间
为单调递减函数.
∴
是递减数列 又
∴数列
中的最大项为
…………12分
六、已知数列
为等差数列，且
（Ⅰ）求数列的通项公式；
（Ⅱ）证明
（I）解：设等差数列
的公差为d.
由
即d=1.
所以
即
（II）证明因为
，
所以
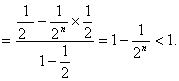
题25. 设{an}是公差d≠0的等差数列，Sn是其前n项的和.
(1)若a1=4，且
，求数列{an}的通项公式；
(2)是否存在
的等差中项？证明你的结论.
(1)由
,
即
,
将a1=4代入上式并整理得d(12+5d)=0,
因为d≠0，解得
.
所以数列{an}的通项公式为
(2)不存在p，q∈N*，且p≠q，使得
的等差中项.
证明：因为
所以
.
因为d≠0，且p≠q,
所以
即不存在p，q∈N*，且p≠q，使得的等差中项.