高一数学必修5练习题(二)
A组题(共100分)
一.选择题:本大题共5题,每小题7分,共35分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设![]() 是等差数列
是等差数列![]() 的前
的前![]() 项和,若
项和,若![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知等差数列![]() 中,
中,![]() ,则该数列前9项和
,则该数列前9项和![]() 等于( )
等于( )
A.18 B.27 C.36 D.45
3.设![]() 是等差数列
是等差数列![]() 的前n项和,若
的前n项和,若![]() ,则
,则![]() =( )
=( )
(A) (B) (C) (D)
4.设![]() 是等差数列,
是等差数列,![]() ,
,![]() ,则这个数列的前6项和等于( )
,则这个数列的前6项和等于( )
A.12 B.24 C.36 D.48
5.已知某等差数列共有10项,其奇数项之和为15,偶数项之和为30,则其公差为( )
A.5 B.4 C. 3 D. 2
二.填空题:本大题共4小题,每小题6分,共24分。
6.设![]() 为等差数列
为等差数列![]() 的前
的前![]() 项和,若
项和,若![]() ,则公差为 .
,则公差为 .
7.在等差数列![]() 中,已知
中,已知![]() ,那么
,那么![]() 等于
.
等于
.
8.正项等差数列![]() 中,
中,![]() 则
则![]() _________.
_________.
9.等差数列![]() 前
前![]() 项和为
项和为![]() ,已知
,已知![]() 为______时,
为______时,![]() 最大. .
最大. .
三.解答题:本大题共3小题,共41分,解答题应写出文字说明、证明过程或演算步骤。
10.已知![]() 是等差数列,其前n项和为
是等差数列,其前n项和为![]() ,已知
,已知![]() 求数列
求数列![]() 的通项公式.(12分)
的通项公式.(12分)
11.等差数列![]() 中,已知
中,已知![]() ,试求n的值.(13分)
,试求n的值.(13分)
12.已知公差大于零的等差数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]()
求数列![]() 的通项公式
的通项公式![]() .(16分)
.(16分)
B组题(共100分)
四.选择题:本大题共5题,每小题7分,共35分。在每小题给出的四个选项中,只有一项是符合题目要求的。
13.等差数列![]() 的公差为d,则数列
的公差为d,则数列![]() (c为常数,且
(c为常数,且![]() )是( )
)是( )
A.公差为d的等差数列 B.公差为cd的等差数列
C.非等差数列 D.以上都不对
14.3、已知![]() 则
则![]() 的等差中项为( )
的等差中项为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
15.4、等差数列![]() 中,
中,![]() ,那么
,那么![]() 的值是( )
的值是( )
A.12 B.24 C.36 D.48
16.等差数列—3,1,5,…的第15项的值是( )
A.40 B.53 C.63 D.76
17.已知等差数列![]() 满足
满足![]() ,则有( )
,则有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
五.填空题:本大题共4小题,每小题6分,共24分。
18.已知数列的通项公式是![]() ,那么当
,那么当![]() 取最小值时,n=______.
取最小值时,n=______.
19.等差数列![]() 的前10项中,项数为奇数的各项之和为125,项数为偶数的各项之和为15,则首项
的前10项中,项数为奇数的各项之和为125,项数为偶数的各项之和为15,则首项![]() =______,公差d=______.
=______,公差d=______.
20.已知数列![]() 为等差数列,且
为等差数列,且![]()
数列![]() 的通项公式为______________________.
的通项公式为______________________.
21. 已知数列![]() 是由正数组成的等差数列,
是由正数组成的等差数列,![]() 是其前n项的和,并且
是其前n项的和,并且![]() ,
,![]() 。数列
。数列![]() 的通项公式为_________________.
的通项公式为_________________.
六.解答题:本大题共3小题,共41分,解答题应写出文字说明、证明过程或演算步骤。
22..已知等差数列![]() ,
,![]() 求
求![]() 的通项公式.
的通项公式.
23.等差数列![]() 的前n项和记为
的前n项和记为![]() .已知
.已知![]()
(Ⅰ)求通项![]() ;(Ⅱ)若
;(Ⅱ)若![]() =242,求n.
=242,求n.![]()
24.已知数列![]() 满足
满足![]() ,
,![]()
![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
C组题(共50分)
七.选择或填空题:本大题共2题。
25.数列![]() 的前n项和
的前n项和![]() ,则
,则![]() .
.
26.数列![]() 满足
满足![]() ,则
,则![]() .
.
八.解答题:本大题共2小题,解答题应写出文字说明、证明过程或演算步骤。
27.数列![]() 满足递推式
满足递推式![]()
(1)求a1,a2,a3;
(2)若存在一个实数![]() ,使得
,使得![]() 为等差数列,求
为等差数列,求![]() 值;
值;
(3)求数列{![]() }的前n项之和.
}的前n项之和.
28.设无穷等差数列![]() 的前n项和为Sn.
的前n项和为Sn.
(1)若首项![]() ,公差
,公差![]() ,求满足
,求满足![]() 的正整数k;
的正整数k;
(2)求所有的无穷等差数列![]() ,使得对于一切正整数k都有
,使得对于一切正整数k都有![]() 成立.
成立.
参考答案
A组题
一.选择题:
1.D 分析:![]() 是等差数列
是等差数列![]() 的前
的前![]() 项和,若
项和,若![]() ∴
∴ ![]()
![]() .
.
2.C 分析:在等差数列![]() 中,
中,![]() ,∴
,∴![]() ,则该数列前9项和
,则该数列前9项和![]() .
.
3.A 分析::由等差数列的求和公式可得![]() 且
且![]()
所以![]() ,故选A.
,故选A.
4.B 分析:![]() 是等差数列,
是等差数列,![]() ∴
∴ ![]() ,则这个数列的前6项和等于
,则这个数列的前6项和等于![]() ,选B.
,选B.
5.C 分析: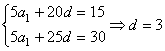 ,故选C.
,故选C.
二.填空题:
6.![]() 分析: 设首项为
分析: 设首项为![]() ,公差为
,公差为![]() ,由题得
,由题得
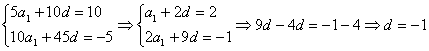
7.4 分析: 略.
8.28 分析: 略.
9.7, 49 分析: 略.
三.解答题:
10.解:(1)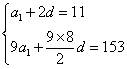 解得:
解得:![]() .
.
11.解:
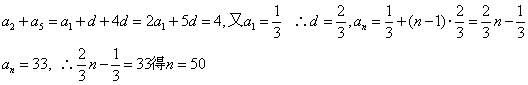
12.解:

B组题
13.B![]()
14.A
15.B
16.B
17.C
18.23
19.113,-22
20.![]() 分析:设等差数列
分析:设等差数列![]() 的公差为d.
的公差为d.
由![]() 即d=1.
即d=1.
所以![]() 即
即![]()
21.![]() 分析:设数列
分析:设数列![]() 的公差为d,由已知得
的公差为d,由已知得![]()
∴(5+d)(10-3d)=28,∴![]() ,解之得d=2或
,解之得d=2或![]() 。
。
∵数列![]() 各项均正,∴d=2,∴
各项均正,∴d=2,∴![]() 。∴
。∴![]() 。
。
22.解:(Ⅰ)设数列![]() 的公差为d,依题意得方程组
的公差为d,依题意得方程组
![]() 解得
解得![]()
所以![]() 的通项公式为
的通项公式为![]()
23.(1)由![]() 得方程组
得方程组
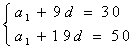 解得
解得![]() 所以
所以 ![]()
(2)由![]() 得方程
得方程![]()
解得![]()
24.![]()
C组题
25.![]()
26.161
27. (1)由![]()
同理求得a2=23, a1=5


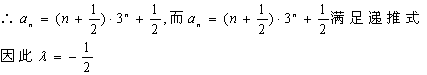
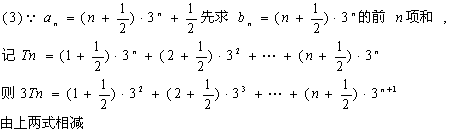
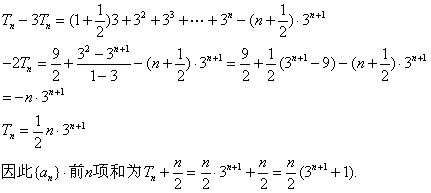
28.解:(1)![]() (2)
(2)![]() 或
或![]() 或
或![]()