高一数学必修5练习题（一）
A组题（共100分）
一．选择题：本大题共5题，每小题7分，共35分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1．已知△ABC中，a＝4，b＝4
，∠A＝30°，则∠B等于( )
A．30° B．30°或150°
C．60° D．60°或120°
2．在△ABC中，已知b＝4
，c＝2，∠A＝120°，则a等于( )
A．2
B．6
C．2或6 D．2
3．已知△ABC中，AB＝6，∠A＝30°，∠B＝120°，则△ABC的面积为( )
A．9 B．18
C．9 D．18
4．在△ABC中，若
，则
等于（ ）
A．1 B．
C．
D．
5．在△ABC中，sinA＞sinB是A＞B的( )
A．充分不必要条件
B．必要不充分条件
C．充要条件
D．既不充分也不必要条件
二．填空题：本大题共4小题，每小题6分，共24分。
6．在△ABC中，若∠B＝30°，AB＝2，AC＝2，则△ABC的面积是________．
7．在△ABC中，若b＝2csinB，则∠C＝________．
8．设△ABC的外接圆半径为R，且已知AB＝4，∠C＝45°，则R＝________．
9．在△ABC中，∠B＝45°，∠C＝60°，a＝2(＋1)，那么△ABC的面积为________．
三．解答题：本大题共3小题，共41分，解答题应写出文字说明、证明过程或演算步骤。
10．在△ABC中，已知
，c=1，
，求a，A，C．（12分）
11．在△ABC中，求证：
（13分）
12．△ABC中，D在边BC上，且BD＝2，DC＝1，∠B＝60o，∠ADC＝150o，求AC的长及△ABC的面积．（16分）
B组题（共100分）
四．选择题：本大题共5题，每小题7分，共35分。在每小题给出的四个选项中，只有一项是符合题目要求的。
13．有一长为1公里的斜坡，它的倾斜角为20°，现要将倾斜角改为10°，则坡底要伸长（ ）
A. 1公里 B. sin10°公里
C. cos10°公里 D. cos20°公里
14．已知在△ABC中，sinA∶sinB∶sinC＝3∶5∶7，那么这个三角形的最大角是( )
A．135° B．90°
C．120° D．150°
15．在△ABC中，已知三边a、b、c满足(a＋b＋c)(a＋b-c)＝3ab，则∠C等于( )
A．15° B．30°
C．45° D．60°
16．已知△ABC中，a∶b∶c＝1∶∶2，则A∶B∶C等于( )
A．1∶2∶3 B．2∶3∶1
C．1∶3∶2 D．3∶1∶2
17．已知△ABC中，sinA∶sinB∶sinC＝k∶(k＋1)∶2k(k≠0)，则k的取值范围为( )
A．(2，＋∞) B．(-∞，0)
C．(-
，0) D．(，＋∞)
五．填空题：本大题共4小题，每小题6分，共24分。
18．已知△ABC中，A＝60°，最大边和最小边是方程x2-9x＋8＝0的两个正实数根，那么BC边长是________．
19．在△ABC中，已知a＝7，b＝8，cosC＝
，则最大角的余弦值是________．
20．已知△ABC的面积为
，且b＝2，c＝，则∠A＝________．
21．在△ABC中，若AB＝
，AC＝5，且cosC＝
，则BC＝________．
六．解答题：本大题共3小题，共41分，解答题应写出文字说明、证明过程或演算步骤。
22．化简
23．在△ABC中，BC＝a，AC＝b，a，b是方程
的两个根，且
。求：(1)角C的度数； (2)AB的长度。
24．
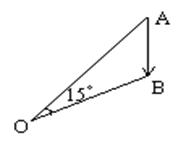在奥运会垒球比赛前，C国教练布置战术时，要求击球手以与连结本垒及游击手的直线成15°方向把球击出，根据经验，通常情况下，球速为游击手最大跑速的4倍，问按这样布置，游击手能否接着球？
C组题（共50分）
七．选择或填空题：本大题共2题。
25．若三角形中有一个角为60°，夹这个角的两边的边长分别是8和5，则它的内切圆半径等于________，外接圆半径等于________．
26．在△ABC中，
＝3，
＝2，与的夹角为60°，则-＝________；＋＝________．
八．解答题：本大题共2小题，解答题应写出文字说明、证明过程或演算步骤。
27．在△ABC中，若
.
(1)判断△ABC的形状；
(2)在上述△ABC中，若角C的对边
，求该三角形内切圆半径的取值范围。
28．
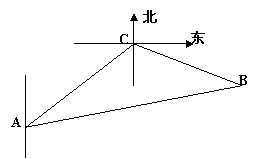一缉私艇发现在北偏东
方向,距离12 nmile的海面上有一走私船正以10 nmile/h的速度沿东偏南
方向逃窜.缉私艇的速度为14
nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东
的方向去追,.求追及所需的时间和
角的正弦值.
参考答案
A组题
一．选择题：
1．D分析：由正弦定理得，
，
∴ sinB＝
，
∴ ∠B＝60°或∠B＝120°．
2．A 分析：由余弦定理得:a2＝b2＋c2-2bccosA＝48＋12-2×4×2×(-)＝84，∴ a＝2．
3．C 分析：∵ ∠A＝30°，∠B＝120°，
∴ ∠C＝30°，∴ BA＝BC＝6，
∴ S△ABC＝×BA×BC×sinB＝×6×6×
＝9．
4．C
5．C 分析：A＞B
a＞b2RsinA＞2RsinBsinA＞sinB．
二．填空题：
6．2或 分析：sinC＝
，于是，∠C＝60°或120°，故∠A＝90°或30°，由S△ABC＝×AB×AC×sinA，可得S△ABC＝2或S△ABC＝．
7．30°或150°分析：由b＝2csinB及正弦定理
，
∴ sinC＝，∴ ∠C＝30°或150°．
8．2
分析：∵ c＝2RsinC，∴ R＝
．
9．6＋2 分析：∵ ，
∴ 
，
∴ b＝4．
∴ S△ABC＝absinC＝6＋2．
三．解答题：
10．a＝
，A＝105°，C＝30°
11．将
，
代入右边即可。
12．
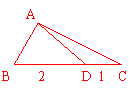1．在△ABC中，∠BAD＝150o－60o＝90o，∴AD＝2sin60o＝
．
在△ACD中，AD2＝()2＋12－2××1×cos150o＝7，∴AC＝
．
∴AB＝2cos60o＝1．S△ABC＝
×1×3×sin60o＝
．
B组题
13．A
14．C 分析：由sinA∶sinB∶sinC＝3∶5∶7知三角形的三边之比为a∶b∶c＝3∶5∶7，最大的边为c，∴ 最大的角为∠C．由余弦定理得
cosC＝
，
15．D 分析：由(a＋b＋c)(a＋b-c)＝3ab，得a2＋2ab＋b2-c2＝3ab
∴ 
，∴ cosC＝60°
16．A 分析：由正弦定理得，
，
∴ sinA∶sinB∶sinC＝1∶∶2＝∶∶1，
∴ A∶B∶C＝30°∶60°∶90°＝1∶2∶3．
17．D 分析：利用正弦定理及三角形两边之和大于第三边．
18．
分析：∵ A＝60°，∴ 最大边和最小边所夹的角为A，AB、AC为x2-9x＋8＝0的两个正实数根，则AB＋AC＝9，AB×AC＝8
∴ BC2＝AB2＋AC2-2×AC×AB×cosA
＝(AB＋AC)2-2×AC×AB×(1＋cosA)
＝92-2×8×＝57
19．-
分析：先由c2＝a2＋b2-2abcosC求出c＝3，∴ 最大边为b，最大角为B，
∴ cosB＝
．
20．60°或120°
分析：∵ S△ABC＝bcsinA，∴ ＝×2×sinA，∴ sinA＝。
21．4或5 分析：设BC＝x，则5＝x2＋25-2·5·x·，即x2-9x＋20＝0，解得x＝4或x＝5
22．原式=
23．解：（1）
C＝120°
（2）由题设：
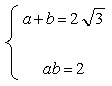
24．不能
C组题
25． 
分析：设60°的角的对边长为x，外接圆半径为R，内切圆半径为r，则x2＝82＋52-2×8×5×cos60°＝49，∴ x＝7
∵ 7＝2Rsin60°，∴ R＝
∵ S△ABC＝×8×5×sin60°＝×r×(8＋5＋7)，∴ r＝
26．
分析：由三角形法则知
-
2＝
2
＝2＋2-2··cosA
＝32＋22-2×3×2×cos60°＝7
∴ -＝
类似地由平行四边形及余弦定理可知
＋2＝32＋22-2×3×2×cos120°＝19
∴ ＋＝
27. 解：（1）由
可得
即C＝90°
△ABC是以C为直角顶点得直角三角形
（2）内切圆半径 
内切圆半径的取值范围是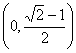
28．解: 设A,C分别表示缉私艇,走私船的位置,设经过 
小时后在B处追上, 则有
,
所以所需时间2小时, 