高一数学直线第一学期期末复习学案
2008年1月3日
班级： 学号 姓名
一、填空题；（每题7分，共70分）
1、经过点
的直线
到A
、B
两点的距离相等，则直线的方程为
2、已知直线与
的倾斜角相等，且与两坐标轴围成的三角形的面积为24，则直线的方程为
3、设A、B两点是
轴上的点，点
的横坐标为2，且
，若直线
的方程为
，则
的方程为
4、若三条直线l1：x－y＝0；l2：x＋y－2＝0; l3：5x－ky－15＝0围成一个三角形，则k的取值范围是
5、已知两定点A(－3，5)，B(2，15)，动点P在直线3x－4y＋4＝0上，则
＋
的最小值为
6、直线
关于点
的对称直线的方程是
7、已知直线过点P
且与以A
、B
为端点的线段相交，则直线的斜率的取值范围为
。
8、已知直线过点A
和B
，则直线的倾斜角的取值范围为
9、已知点P到两定点M
、N
的距离之比为
，点N到直线PM的距离为1，则直线PN的方程为
。
10、已知直线的斜率为6，且被两坐标轴所截的的线段长为
，则直线的方程为
二、解答题：（每题15分，共30分）
11、已知两直线
定点A
，若直线过
与
的交点且与点A的距离等于1，求直线的方程
12、已知直线过点P
且与轴、
轴的正半轴相交与A、B两点，求
面积最小值及这时直线的方程
江苏省沭阳高级中学2007~2008学年度第一学期期末复习学案
直线参考答案 2008年1月3日
一、填空题；（每题7分，共70分）
1、
或
2、
，
3、
4、
5、
6、
7、
8、
9、
，
，
10、
，
，
二、解答题：（每题15分，共30分）
11、已知两直线定点A，若直线过与的交点且与点A的距离等于1，求直线的方程
解：
方法一：
的交点为
，若所求直线斜率存在，设所求的直线方程为
即
因为所求的直线与点A的距离为1，所以
，得
所以所求的直线的方程为
若所求直线斜率不存在时，即为
，
因为点A到直线为的距离为1，所以直线也满足题意
所以所求的直线的方程为或
方法二：的交点为（
2
1）
过 交点的直线系方程是
，
是参数
化简的
，③
由
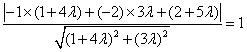得
代入方程③ 得
又因为直线系方程③ 中不包括 ，所以应检查是否也符合所求的条件
点到的距离为
也符合条件，
所求直线的方程是和。
12、已知直线过点P且与轴、轴的正半轴相交与A、B两点，求面积最小值及这时直线的方程
、解：方法一：设
则直线的方程为：
，
过点
，
从而
，
故有
当且仅当
，即
时，
，
此时
，直线的方程为
即
。
方法二：依题意知，直线的斜率存在且
设直线的方程为
，
则有
当且仅当
时 ,即
时，等号成立
故所求直线的方程为。