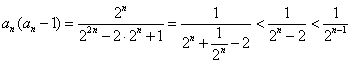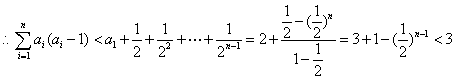高一年级数学第二学期期中考试
数 学 试 题 2008.4.28.
一、填空题:本大题共14小题,每小题5分,共70分,
1、已知等差数列![]() 中,
中,![]() ,
,![]() ,则
,则![]() 。
。
2、已知![]() ,则
,则![]() 的取值范围为 。
的取值范围为 。
3、在等比数列{an}中,a2=8,a1=64,,则公比q为 。
4、已知等差数列![]() 中,
中,![]() ,则
,则![]() 。
。
5、在△ABC中,已知![]() ,
,![]() ,
,![]() ,则
,则![]() 。
。
6、在![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() ,若
,若![]() ,b=
,b=![]() ,
,![]() ,则
,则![]() 。
。
7、已知数列的通项![]() ,则其前
,则其前![]() 项和
项和![]() 。
。
8、若点![]() 在直线
在直线![]() 的下方,则
的下方,则![]() 的取值范围为 。
的取值范围为 。
9、若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,则
,则![]() 。
。
10、点![]() 在不等式组
在不等式组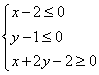 表示的平面区域上运动,则
表示的平面区域上运动,则![]() 的最大值为
。
的最大值为
。
11、数列![]() 满足
满足![]() ,则
,则![]() 。
。
12、二次函数y=ax2+bx+c(x∈R)的部分对应值如下表:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
则不等式ax2+bx+c>0的解集是 .
13、一同学在电脑中打印如下若干个圆(图中●表示实圆,○表示空心圆);
●○●●○●●●○●●●●○●●●●●○●●●●●●○……,若依此规律继续打下去,那么在前2008个圆中,有 个空心圆。
14、已知![]() ,则当
,则当![]() 取最小值时,
取最小值时,![]() 的值是 .
的值是 .
二、解答题(本大题共6道题,计90分)
15、(本题满分14分)已知关于![]() 不等式
不等式![]() 解集为
解集为![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
16、(本题满分14分)记关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,不等式
,不等式![]() 的解集为
的解集为![]() .
.
(I)若![]() ,求
,求![]() ;(II)若
;(II)若![]() ,求正数
,求正数![]() 的取值范围.
的取值范围.
17、(本题满分14分)设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,![]() .
.
(Ⅰ)求B的大小;(Ⅱ)若![]() ,
,![]() ,求b及
,求b及![]() .
.
18、(本题满分16分)设![]() 是公比大于1的等比数列,
是公比大于1的等比数列,![]() 为数列
为数列![]() 的前
的前![]() 项和.已知
项和.已知![]() ,且
,且![]() 构成等差数列.
构成等差数列.
(1)求数列![]() 的通项公式.
的通项公式.
(2)令![]() 求数列
求数列![]() 的前
的前![]() 项和
项和![]() .
.
19、(本题满分16分)本公司计划2008年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为![]() 元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
20、(本题满分16分)在数列![]() 中,已知
中,已知![]() ,
,![]() .
.
(1)证明数列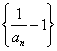 为等差数列,并求数列
为等差数列,并求数列![]() 的通项公式;
的通项公式;
(2)求证:![]() .
.
高邮市车逻中学高一期中考参考答案
1、![]() 2、
2、![]() 3、
3、![]() 4、10 5、
4、10 5、![]() 6、
6、![]()
7、![]() 8、
8、![]() 9、
9、![]() 10、2 11、
10、2 11、![]()
12、![]() 13、61 14、3
13、61 14、3
15、当![]() 时,显然不适合题意,故
时,显然不适合题意,故![]() ,由题意得:
,由题意得: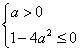 即:
即:![]()
16、解:(I)由![]() ,得
,得![]() .
.
(II)![]() .由
.由![]() ,得
,得![]() ,又
,又![]() ,所以
,所以![]() ,
,
17、解:(Ⅰ)由![]() ,根据正弦定理得
,根据正弦定理得![]() ,所以
,所以![]() ,
,
由![]() 为锐角三角形得
为锐角三角形得![]() .
.
(Ⅱ)根据余弦定理,得![]()
![]()
![]() .所以,
.所以,![]() .
.
![]() 。
。
18、解:(1)由已知得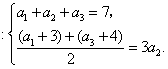 解得
解得![]() .
.
设数列![]() 的公比为
的公比为![]() ,由
,由![]() ,可得
,可得![]() .
.
又![]() ,可知
,可知![]() ,即
,即![]() ,
,
解得![]() .由题意得
.由题意得![]() .
.![]() .故数列
.故数列![]() 的通项为
的通项为![]() .
.
(2)由于![]() 由(1)得
由(1)得![]()
![]() , 又
, 又![]()
![]() 是等差数列.
是等差数列.
![]()
![]() 故
故![]() .
.
19、解:设公司在甲电视台和乙电视台做广告的时间分别为![]() 分钟和
分钟和![]() 分钟,总收益为
分钟,总收益为![]() 元,由题意得
元,由题意得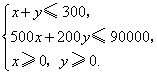
 目标函数为
目标函数为![]() .
.
二元一次不等式组等价于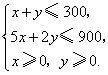
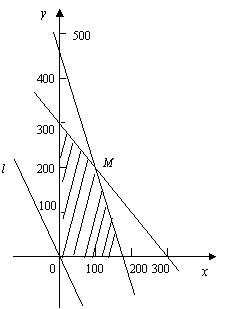
作出二元一次不等式组所表示的平面区域,即可行域.
如图:
作直线![]() , 即
, 即![]() .
.
平移直线![]() ,从图中可知,当直线
,从图中可知,当直线![]() 过
过![]() 点时,目标函数取得最大值.
点时,目标函数取得最大值.
联立![]() 解得
解得![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() .
. ![]() (元)
(元)
答:该公司在甲电视台做100分钟广告,在乙电视台做200分钟广告,公司的收益最大,最大收益是70万元.
20:(1)![]()
![]()
故数列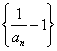 是以
是以![]() 为首项,公比为
为首项,公比为![]() 的等比数列;
的等比数列;
即:![]()
![]()
(2)法一:![]()
![]()
![]()
![]()
法二: