高一数学上中期考试题
高2010级数学
命题人:毛胜红 审题人:邬开友
第Ⅰ卷(选择题,共50分)
一、选择题(本题共10小题,每小题5分,共50分.在每小题给出的四个备选项中,只有一项是符合题目要求的.把答案填涂在机读卡相应位置.)
1.方程组![]() 的解集为…………………………………………………( )
的解集为…………………………………………………( )
A. {2,1} B. {1,2} C. {(2,1)} D.(2,1)
2.已知全集U={-2,-8,0,π,6, 10},集合A={-2,π,6},B={1},
则(![]() UA)∪B等于………………………………………………………………(
)
UA)∪B等于………………………………………………………………(
)
A. {0,1,-8,10} B. {1,-2,π,6} C. {0,-8,10} D. Φ
3.若函数![]() 在其定义域上是增函数,则………………( )
在其定义域上是增函数,则………………( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
4.函数![]() 的图象是………………………………………………………( )
的图象是………………………………………………………( )
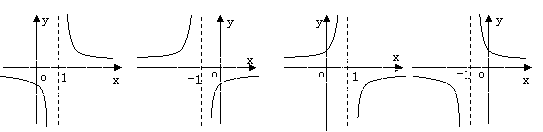
A B C D
5.函数![]() 的最小值为………………………………………………( )
的最小值为………………………………………………( )
A.0 B.![]() C.1
D.
C.1
D.![]()
6.设原命题“若p则q” 假而逆命题真时,则p是q的………………………( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
7.已知从甲地到乙地通话m分钟的电话费由函数![]() 元给出,其中
元给出,其中![]() ,[m]表示不超过m的最大整数,(如[3]=3,[3.2]=3),则从甲地到乙地通话时间为5.5分钟的话费为………………………………………………………………………( )
,[m]表示不超过m的最大整数,(如[3]=3,[3.2]=3),则从甲地到乙地通话时间为5.5分钟的话费为………………………………………………………………………( )
A.4.77 B.4.24 C.3.97 D.3.71
8.设![]() 和
和![]() 是两个集合,定义集合
是两个集合,定义集合![]() ,如果
,如果![]() ,
,![]() ,那么
,那么![]() 等于…………………………………………( )
等于…………………………………………( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.函数![]() 的图象和函数
的图象和函数![]() 的图象的交点个数是…………………………………………………………………………………(
)
的图象的交点个数是…………………………………………………………………………………(
)
A. 4 B. 3 C. 2 D. 1
10.若条件![]() :函数
:函数![]() 有意义;条件
有意义;条件![]() :关于
:关于![]() 的方程
的方程![]() 至多有一个实数根。则
至多有一个实数根。则![]() 是
是![]() 的…………………………………………………( )
的…………………………………………………( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
第Ⅱ卷(非选择题,共100分)
二、填空题(本题共6小题,每小题4分,共24分.把答案写在答题卡相应位置.)
11.经调查,我校某班62名学生中,有37名喜欢语文,49名喜欢数学,两门都喜欢的有30名,则两门都不喜欢的有 名学生。
12.设![]() ,集合
,集合![]() ,则
,则![]() .
.
13.函数![]() 的定义域是
.
的定义域是
.
14.函数![]() 在(-2,+∞)上是减函数,则实数
在(-2,+∞)上是减函数,则实数![]() 的取值范围是__________.
的取值范围是__________.
15.设函数![]() 对于任意
对于任意![]() 都有
都有![]()
![]() ,则
,则![]() = .
= .
16、在下列五个命题中:
①若![]() ,则
,则![]() ;
;
②若P={x0![]() x
x ![]() 4},Q={
y 0
4},Q={
y 0![]() y
y ![]() 2},则对应y=
2},则对应y=![]() 不是从P到Q的映射;
不是从P到Q的映射;
③![]() 在(-
在(-![]() ,0)∪(0,+
,0)∪(0,+![]() )上为减函数;
)上为减函数;
④若函数![]() 的图象经过点
的图象经过点![]() ,则函数
,则函数![]() 的图象必经过点(1,3);
的图象必经过点(1,3);
⑤命题“对任意的![]() ,
,![]() ”的否定是“不存在
”的否定是“不存在![]() ,
,![]() ”;
”;
其中所有不正确的命题的序号为 。
三、解答题(本大题共6小题,共76分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分13分)已知集合A=![]() ,集合B=
,集合B=![]() ,集合C=
,集合C=![]() ;
;
(1)求![]() ;(2)如果
;(2)如果![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
18.(本小题满分13分)已知函数![]() =
=![]() (
(![]() ≠-
≠-![]() ,
,![]() ≠
≠![]() ).
).
(1)求![]() 的反函数
的反函数![]() ;(2)若函数
;(2)若函数![]() 的图象关于直线
的图象关于直线![]() =
=![]() 对称,求实数
对称,求实数![]() 的值.
的值.
19.(本小题满分12分)设![]() 不等式
不等式![]() 的解集是(-3,2).
的解集是(-3,2).
(1)求![]() ;(2)当函数
;(2)当函数![]() 的定义域是[-1,1]时,求函数
的定义域是[-1,1]时,求函数![]() 的值域.
的值域.
20.(本小题满分12分)已知命题p:![]() 有两个不相等的负数根;命题q:方程
有两个不相等的负数根;命题q:方程![]() 无实根,若“p或q”为真,而“p且q”为假,求实数m的取值范围.
无实根,若“p或q”为真,而“p且q”为假,求实数m的取值范围.
21. (本小题满分12分)已知![]() ,
,
(1)若![]() ,求实数
,求实数![]() 的值;
的值;
(2)若关于![]() 的方程
的方程![]() 的两个根
的两个根![]() 满足
满足![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
22.(本小题满分14分)
探究函数![]() 的最小值,并确定取得最小值时
的最小值,并确定取得最小值时![]() 的值.列表如下:
的值.列表如下:
|
| … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
|
| … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
请观察表中值![]() 随
随![]() 值变化的特点,完成以下的问题.
值变化的特点,完成以下的问题.
函数![]() 在区间(0,2)上递减;
在区间(0,2)上递减;
函数![]() 在区间
上递增.
在区间
上递增.
当![]() 时,
时,![]() .
.
证明:函数![]() 在区间(0,2)递减.
在区间(0,2)递减.
思考: (直接回答结果,不需证明)
(1)函数![]() 有没有最值?如果有,请说明是最大值还是最小值,以及取相应最值时
有没有最值?如果有,请说明是最大值还是最小值,以及取相应最值时![]() 的值。
的值。
(2)函数![]() 在区间
和
上单调递增。
在区间
和
上单调递增。
重庆市江北中学校2007-2008学年(上)中期考试
高2010级数学答题卷
二、填空题(本题共6小题,每小题4分,共24分.
11. ; 12. ; 13. ;
14. ; 15. ; 16. .
三、解答题(本大题共6小题,共76分.解答应写出文字说明、证明过程或演算步骤)
17. (本小题满分13分)
解:
18. (本小题满分13分)
解:
19. (本小题满分12分)
解:
20. (本小题满分12分)
解:
21. (本小题满分12分)
解:
22. (本小题满分14分)
探究函数![]() 的最小值,并确定取得最小值时
的最小值,并确定取得最小值时![]() 的值.列表如下:
的值.列表如下:
|
| … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
|
| … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
请观察表中值![]() 随
随![]() 值变化的特点,完成以下的问题.
值变化的特点,完成以下的问题.
函数![]() 在区间(0,2)上递减;
在区间(0,2)上递减;
函数![]() 在区间
上递增.
在区间
上递增.
当![]() 时,
时,![]() .
.
求证:函数![]() 在区间(0,2)递减.
在区间(0,2)递减.
证明:
思考: (直接回答结果,不需证明)
(1)函数![]() 有没有最值?如果有,请说明是最大值还是最小值,以及取相应最值时
有没有最值?如果有,请说明是最大值还是最小值,以及取相应最值时![]() 的值。
的值。
(2)函数![]() 在区间
和
上单调递增。
在区间
和
上单调递增。
参考答案
1~10:CAADC,BDDBA。
11: 6 ;12: 2 ;13:
![]() ;14:
;14:
![]() ;15:
-6 ;16: ①③⑤。
;15:
-6 ;16: ①③⑤。
17解:(1)A={x1≤x<7}…………………………… ……………6分
A∪B={x1≤x<10}………………………………………9分
(2)当![]() 时满足A∩C≠φ……………………………13分
时满足A∩C≠φ……………………………13分
18.解:(1)设y=![]() ,则y(x+a)=3x+1,…………………………2分
,则y(x+a)=3x+1,…………………………2分
整理得(y-3)x=1-ay.……………………………………………3分
若y=3,则a=![]() ,与已知矛盾,
,与已知矛盾,
∴![]() …………………………………………………………4分
…………………………………………………………4分
∴![]() =
=![]() .……………………………………………………5分
.……………………………………………………5分
故所求反函数为f-1(x)= ![]() (x≠3).……………………7分
(x≠3).……………………7分
(2)依题意得f--1(x)=f(x),则![]() =
=![]() ,………………10分
,………………10分
整理得3x2-8x-3=-ax2+(1-a2)x+a,
比较两边对应项的系数,…………………… ………………11分
有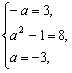
故a=-3.…………………………………………………………13分
19.解:(1)
∵不等式![]() 的解集是(-3,2)即
的解集是(-3,2)即![]() 的解集是(-3,2)
的解集是(-3,2)
∴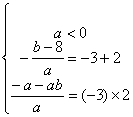 …………………………………………3分
…………………………………………3分
解得![]() ………………………… ……………………5分
………………………… ……………………5分
∴![]() ……………………………………………7分
……………………………………………7分
(2)结合二次函数的图像与性质可知函数![]() 在区间
在区间![]() 上是增函数,在区间
上是增函数,在区间![]() 上是减函数,所以
上是减函数,所以
当![]() ………………12分
………………12分
20. 解:命题p为真时, 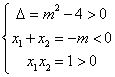 …………………………3分
…………………………3分
解得 m>2……………………………………………………………………5分
命题q为真时,![]()
![]() . …7分
. …7分
又∵“p或q”为真,“p且q”为假,∴ p,q必为一真一假, ……9分
∴1<m![]() 2或3
2或3![]() m.…………………………………………………………12分
m.…………………………………………………………12分
21. 解:(1)∵![]()
![]() ,
,![]()
∴![]() ,
,![]() …………………4分
…………………4分
比较两边对应项的系数,有
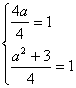
∴![]() ……………………………………………………………………6分
……………………………………………………………………6分
(2)因为![]() ……8分
……8分
所以关于![]() 的方程
的方程![]() 的两个根
的两个根![]() 满足
满足![]() 也就是关于
也就是关于![]() 的方程
的方程![]() 的两个根
的两个根![]() 满足
满足![]() ……………………………9分
……………………………9分
设![]() ,由二次函数的图像与性质可知
,由二次函数的图像与性质可知
![]()
即![]() ……………………………………………………………………11分
……………………………………………………………………11分
∴![]() ………………………………………………………………… ……12分
………………………………………………………………… ……12分
22.(1)函数![]() 在区间
在区间 ![]() 上递增.…… ………2分
上递增.…… ………2分
当![]() 2 时,
2 时,![]() 4 .………………………4分
4 .………………………4分
求证:函数![]() 在区间(0,2)递减.
在区间(0,2)递减.
证明:
设![]() 是区间,(0,2)上的任意两个数,且
是区间,(0,2)上的任意两个数,且![]() ………5分
………5分
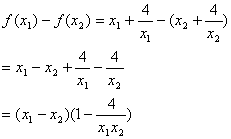
![]() ………………………………………7分
………………………………………7分
![]()
∴![]()
又![]()
∴![]() ……………………………… …………8分
……………………………… …………8分
∴![]()
![]()
∴函数在(0,2)上为减函数.………………… …………9分
思考: (直接回答结果,不需证明)
(1)函数![]() 有没有最值?如果有,请说明是最大值还是最小值,以及取相应最值时
有没有最值?如果有,请说明是最大值还是最小值,以及取相应最值时![]() 的值。
的值。
答:![]() 有最值,当
有最值,当![]() 时,
时,![]() ………………11分
………………11分
(2)函数![]() 在区间
在区间 ![]() 和
和
![]() 上单调递增。
上单调递增。
………………………………………………………………………………………14分