高一数学下册3月月考试题

高一数学下册3月月考试题　　　　　　　　　　　　　 2008.03.08

一、填空题：

1．在等差数列{a_n}中，已知a₅＝10，a₁₂＝31，则首项是_______－2，公差是_______3.

2．在△ABC中，已知A＝105⁰，B＝30⁰，b＝2，则c等于___________　4 

3．在△ABC中，若sin²A＝sin²B＋sin²C＋sinB·sinC，则角A=________ 　　

4．在△ABC中，已知a＝7，b＝8，cosC＝，则最大角的余弦值是________-　

5．在中，，，，则的面积为____________　　 6．在△ABC中，若∠B＝30°，AB＝2，AC＝2，则△ABC的面积是________2或

7． a、b、c为△ABC的三边，其面积S_△ABC＝12，bc＝48，b－c＝2，则a=______　　　　　　　　　　　　　　　　　　　　　　　　　　 2或2

　　　　

8．在△ABC中，若b＝2csinB，则∠C＝________30°或150°

9．已知△ABC的面积为，且b＝2，c＝，则∠A＝__________60°或120°

10．在△ABC中，若AB＝，AC＝5，且cosC＝，则BC＝__________4或5　　　

11．在△ABC中，a、b、c分别为A、B、C的对边，，则△ABC的形状为______直角三角形

12．已知f(n＋1)＝f(n)－(n∈N^*)且f(2)＝2，则f(101)＝_______－ 

13．若三角形中有一个角为60°，夹这个角的两边的边长分别是8和5，则它的内切圆半径等于________　外接圆半径等于________

　　分析：设60°的角的对边长为x，外接圆半径为R，内切圆半径为r，则x²＝8²＋5²-2×8×5×cos60°＝49，∴　x＝7

　　∵　7＝2Rsin60°，∴　R＝

　　∵　S_△ABC＝×8×5×sin60°＝×r×(8＋5＋7)，∴　r＝

二、解答题：

14．已知数列{a_n}为等差数列，a₃＝，a₇＝－，求a₁₅的值.

利用通项公式，设数列{a_n}的首项为a₁,公差为d

则　 解之得

a₁₅＝a₁＋14d＝＋14×(－)＝－

15．已知三个数成等差数列，其和为15，其平方和为83，求此三个数.

解：设此三数分别为x－d、x、x＋d

则

解得x＝5，d＝±2.

∴所求三个数列分别为3、5、7或7、5、3.

16．数列通项公式为a_n＝n²－5n＋4，问

（1）数列中有多少项是负数？（2）n为何值时，a_n有最小值？并求出最小值.

（1）由a_n为负数，得n²－5n＋4<0，解得1<n<4.

∵n∈N^*，故n＝2或3，即数列有2项为负数，分别是第2项和第3项.

（2）∵a_n＝n²－5n＋4＝(n－)²－，∴对称轴为n＝＝2.5

又∵n∈N^*，故当n＝2或n＝3时，a_n有最小值，最小值为2²－5×2＋4＝－2.

17．△ABC中，D在边BC上，且BD＝2，DC＝1，∠B＝60^o，∠ADC＝150^o，求AC的长及△ABC的面积．

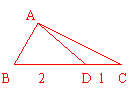在△ABC中，∠BAD＝150^o－60^o＝90^o，∴AD＝2sin60^o＝．

在△ACD中，AD²＝()²＋1²－2××1×cos150^o＝7，∴AC＝．

∴AB＝2cos60^o＝1．S_△ABC＝×1×3×sin60^o＝．

18．在△ABC中，已知a＝，b＝，B＝45°，求A，C及c.

解：∵＝，∴sinA＝＝＝

∵b＜a且b＞asinB

∴A有两解：A＝60°或120°.

（1）当A＝60°时，C＝180°－（A+B）＝75°

 c＝＝＝

(2)当A＝120°时，C＝180°－（A+B）＝15°

c＝＝＝.

19．在△ABC中，a、b、c分别是角A、B、C所对的边长，若a²＋c²＝b²＋ac且＝，求角C的大小.

【解】 由a²＋c²＝b²＋ac得：cosB＝＝＝，所以，B＝60°

又∵＝

∴＝＝＝cotC＋＝

∴cotC＝1，C＝45°.

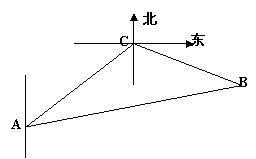20．一缉私艇发现在北偏东方向,距离12 nmile的海面上有一走私船正以10 nmile/h的速度沿东偏南方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东的方向去追,.求追及所需的时间和角的正弦值.

28．解:  设A,C分别表示缉私艇,走私船的位置,设经过  小时后在B处追上,　则有

,

所以所需时间2小时,