高一数学下册第二次周练试卷

　　　　高一数学下册第二次周练试卷

一．填空题

1．在△ABC中,AB=3,BC=,AC=4,则边AC上的高为_____________

2．在△ABC中,若sinA:sinB:sinC=3:2:4,则cosC的值为____________

3．已知a,b,c是△ABC中A,B,C的对边,S是△ABC的面积,若a=4,b=5,S=,则c的长度为　　　　 

4．在等差数列中，已知++=39，++=33，则++=________ 5．在等比数列中,则__________

6．某种细菌在培养过程中，每20分钟分裂一次，(一个分裂成二个)则经过3小时， 由1个这种细菌可以繁殖成____________

7．已知数列的通项公式为，那么是这个数列的第________项．

8．等比数列的公比为2, 且前4项之和等于1, 那么前8项之和等于　　　　 　.　

9．不等式-x²+3x-5≥0的解集是____________

10．不等式  的正整数解集是　　　　　　　　

11．已知集合，则集合=_________

12．不等式的解集是___________

13．已知不等式x²-2x-3<0的解集为A, 不等式x²+x-6<0的解集是B, 不等式x²+ax+b<0的解集是AÇB, 那么a+b等于____________　　　　　　　　　　　　　　　　　　　　　 

14．不等式ax²+bx+c>0的解集为{xx<-1,或x>2}, 那么不等式ax²-bx+c>0的解集是_________．

二．解答题

15．(1)解不等式：　　 (2)解不等式组：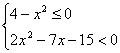

16．若a,b,c是△ABC中A,B,C的对边,A、B、C成等差数列, a,b,c成等比数列，试判断△ABC的形状。

17．如图所示,我舰在敌岛A南偏西50^o 相距12海里的B处，发现敌舰正由岛A沿北偏西10^o的方向以时速10海里航行，我舰要用2小时在C处追上敌舰，问需要的速度是多少？

18．解关于x的不等式x²-(a+a²)x+a³>0．　

19．若不等式mx²+2(m+1)x+9m+4<0的解集为R, 求实数m的取值范围．

20．已知集合A={a关于x的方程x²-ax+1=0,有实根}，B={a不等式ax²-x+1>0对一切xR成立},求AB．

金沙中学高一数学第二次周练试卷参考答案

1．　　2. 　　3．　　4. 27　　5. -4　 6. 512　　7. 3　　8. 17　 9．F 　　 10、

11．{}　　12．（-7，3）　　13．-3　　　14．{xx>1或x<-2}

15、(1)  (2)

16、解:

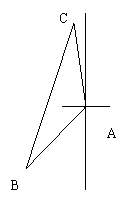17、解: 我舰2小时后在C处追上敌舰,即

18．原不等式变形(x-a)(x-a²)>0．

　  ①　当a>1或a<0时, 有a²>a, 故原不等式解集为{xx>a²或x<a}；

　  ②　当0<a<1时, 有a²<a, 故原不等式解集为{xx>a或x<a²}；

　  ③　当a=0或a=1时, 有a²=a, 故原不等式解集为{xx¹a}．

19．分类讨论：①当m=0时, 原不等式变为2x+4<0, 显然它的解集不是R,所以m=0不满足条件

　②当m¹0时, 只要满足 D=[2(m+1)]²-4m(9m+4)<0，且m<0即可, 解得m<- ．由①②知, m<-

20．{a}．