必修2—3空间直角坐标系检测题（B卷）
姓名 得分
一．选择题
1．在空间直角坐标系中，设
为任意实数，相应的点
的集合确定的图形为
（ ）
A．点 B．直线 C．圆 D．平面
2．已知点
，那么点
关于
轴对称点的坐标是
（ ）
A．
B．
C． 
D．
3．点
在
平面上的投影点
的坐标是
（ ）
A．
B．
C．
D． 
4．已知点
，则
的形状是
（ ）
A．等腰三角形 B．等边三角形 C．直角三角形 D．等腰直角三角形
5．已知
，记到
轴的距离为
，到轴的距离为
，到轴的距离为
，则（ ）
A．
B．
C．
D．
6. 在直角坐标系中，已知两点
，沿轴把直角坐标平面折成直二面角后，
两点的距离为
( )
A．
B．
C．
D．
二．填空题
7．点
是点
关于轴的对称点，则线段
长为
。
8．已知三角形的三个顶点
，则过点
的中线长为
。
9．已知正四棱柱
的顶点坐标分别为
，
，则
的坐标为
。
10．已知球面
，与点
，则球面上的点与点距离的最大值与最小值分别是
。
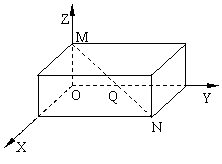三．解答题
11．如图，已知长方体中心
，求的坐标及
的长度。
点
的坐标为
；所以的长度为：
。
12．已知三点
，这三点能共线吗？若能共线，求出的值；若不能共线，说明理由。
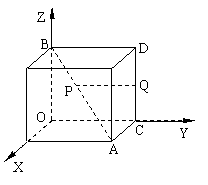13．如图，以棱长为的正方体的三条棱为坐标轴，建立空间直角坐标系
，点
在正方体的对角线上，点
在正方体的棱
上。
（1）当点为对角线的中点，点在棱上运动时，
探究
的最小值；
（2）当点在对角线上运动，点为棱的中点时，
探究的最小值；
（3）当点在对角线上运动，点在棱上运动时，探究的最小值
B卷答案与提示
一．选择题
1．答案：B
提示：表示与
面垂直的直线。
2．答案：B
3．答案：B
提示：平面上点的坐标特征是
。
4．答案：C
提示：根据两点间距离公式
，则有
。
5．答案：B
提示：到轴的距离
，到轴的距离
，到轴的距离
，
所以。
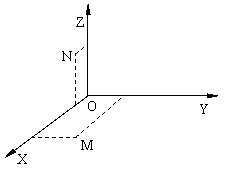
6．答案：C
提示：翻折后，建立如图所示的空间直角坐标系，
两点的坐标分别为：
，
利用空间直角坐标系中两点间距离公式得，
两点的距离为：
二．填空题
7．答案：
提示：点的坐标为
，所以根据两点间距离公式，线段长为。
8．答案：7
提示：
的中点坐标为
，所以过点的中线长为7。
9．答案：
提示：
点坐标为
，因为，所以将点沿轴正方向平移5个单位，就得到点的坐标，所以点的坐标为。
10．答案：9与3
提示：球心为
，半径为3，所以点到球心距离为6，所以球面上的点与点距离的最大值与最小值分别是：9与3
三．解答题
11．解：设点的坐标为
，点的坐标为
，长方体中心为的中点，利用中点坐标公式可得，
，所以点的坐标为
，
12．解：根据空间直角坐标系两点间距离公式，
，
，
，
因为
，所以若
三点共线，则
或
，
若，整理得：
，此方程无解；
若，整理得：，此方程也无解。
所以三点不能共线。
13．解：由已知
，
（1）当点为对角线的中点时，点坐标为
，
设
，则
，
当
时，取到最小值为
，此时为的中点。
（2）当点为棱的中点时，点的坐标为
，设
，则
，
，
，所以点的坐标为
，
所以
，当
，即为的中点时，取到最小值。
（3）当点在对角线上运动，点在棱上运动时，设，
则设
，
，所以
，
所以当且
，即
分别为
中点时，取到最小值为。