高一上册半期考试数学试题及答案
第一卷
一:选择题(每题5分共60分,每题只有一个正确答案)
1.下列函数中为指数函数的是( D )
2. 有五个关系式：①
；②
；③
；④
；⑤
其中正确的有
（
B ）
A.1个. B.2个.
C.3个.
D.4个.
3.关于从集合A到集合B的映射，下面的说法错误的是 ( B )
A． A中的每一个元素在B中都有象
B． A中的两个不同的元素在B中的象必不同
C． B中的元素在A中可以没有原象
D． B中的某元素在A中的原象可能不止一个
4. 全集 U = { 0, －1, －2, －3, －4 }，集合 M = { 0, －1, －2 }，
N = { 0, －3, －4 }，则 ( C U M )∩N 为 ( B )
A. { 0 } B. {－3, －4 } C. {－1, －2 } D. φ
5.下列函数中，值域是 
0 , + ∞ ) 的是
( D )
A.
y =
B.
y = 2x + 1 ( x ＞0 )
C. y = x
2 + x + 1 D. y =
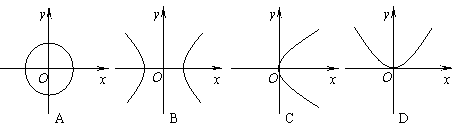
6. 下列各图形中，是函数的图象的是( D )
7.给出下列函数：（1）y=
; (2) y=x; x
; (3) y=x2+
; (4)y=x2+c
其中偶函数的有（ B ）
A . 1个 B. 2个 C. 3个 D. 4个
8.满足条件 { 0, 1 }∪A = { 0, 1 } 的所有的集合A的个数是( D )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
9.已知函数
的定义域是
,
,当
时,
是单调递减;当
时,是单调递增,则 的最小值为(
B )
10全集U={1,2,3,
,9}
则B=( D )
11. 设函数
则关于x的方程
解的个数为 （ C ）
A．1 B．2 C．3 D．4
12.已知二次函数
在
是单调递减函数,则
的取值范围是( C )
第一卷
一.选择题答案
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | B | B | B | D | D | B | D | B | D | C | C |
第二卷
二:填空题(每题4分16分) 总分_______________
13.函数f(x)=
的定义域是
14.已知
,则
1
15.已知f(x)=x2+1, 则f(x+1)=
.
16. 已知全集U={三角形}，A={直角三角形}，则CUA=
三:解答题(6题74分)
17. 已知全集为R,集合A={
},B={
}
(1)
(用区间表示) (2)若
,求
(3)若
,求a的取值范围；(13分)
解: (1) =
(4分)
(2)
当
则
=
(9分)
(3)用数轴分析得
,且
(13分)
18.已知的定义域为
,当
时的图像为线段,当
时的图像为抛物线的一部分,且顶点为
.又已知
,求的解析式(13分)
解: 当时的图像为线段,设
(2分)
由已知故
时
.
(6分)
当时的图像为抛物线的一部分, 且顶点为
设
,又
(8分)
当时
(12分)
(13分)
19.已知
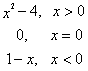(12分)
(1) 求
,
,(2)画出的图像
(2) 若
,问为何值时,方程没有根?有一个根?两个根?
解.(1). 
(4分)
(2)略 (8分)(画错一段扣2分,画错两段扣4分)
(3)由图像观察得
,无解
当
且
时只有一个根
当
,或
时有两个根 (12分)
20设A=
, B=
其中a
,如果A
B=B,求实数a 的范围(12分)
解.由条件得
由AB=B得
(1)
,方程
无解,
则
得
(4分)
(2)
,则
,得
,或
检验,满足条件
(8分)
(3)
,则
得或
检验不合条件舍去
(12分)
(没有检验的扣2分)
21.已知函数
，
（
为正常数），且 (12分)
函数
与
的图象交点在
轴上。
(1)求的值； (2)判断
的奇偶性;
(3)求函数的最小值;
解. (1)的图象与轴交点为(0,1), 过(0,1)点
(3分)
(2)
由(1)得
=
,
,又
为非奇非偶函数(7分)
(3)当
时=
在
单调递增, 
,最小为4.
当
时, =
=
当
时最小为
(11分)
综上当时最小为(12分)
22.已知函数
(
)(12分)
(1)
若能表示成一个奇函数
和一个偶函数
的和,求和的解析式
(2)
若函数在区间
上是增函数;函数是减函数,求的取值范围;
(3)
在满足(2)的条件下,比较
与
的大小
解.(1) =
=
=
=
(4分)
(2) 的对称轴为
函数在区间上是增函数
.
又=是减函数
,
(8分)
(3) 
<0且
的对称轴为
都在
内,且
(10分)
>
(12分)