高一上学期期末数学复习试卷
一、选择题
1、下列各组中的两个集合M和N, 表示同一集合的是（ D ）.
A. 
, 
B.
, 
C. 
, 
D. 
, 
2、直线
的倾斜角是( A )
（A）30° （B）120° （C）60° （D）150°
3、与
为同一函数的是（ B ）.
A．
B. 
C. 
D. 
4、设
, 用二分法求方程
内近似解的过程中,
计算得到
则方程的根落在区间（ B ）.
A.（1,1.25） B.（1.25,1.5） C.（1.5,2） D.不能确定
5、下列各式错误的是（ C ）.
A. 
B. 
C. 
D. 
6、设集合
,
，若
，则
的取值范围是（ B ）
A．
B．
C．
D．[－1，2]
7、直线L1:ax+3y+1=0, L2:2x+(a+1)y+1=0, 若L1∥L2,则a=( C )
A．-3 B．2 C．-3或2 D．3或-2
8、点P(x,y)在直线x+y-4=0上，O是坐标原点，则│OP│的最小值是（ C ）
A． B. C.2 D.
9、圆锥平行于底面的截面面积是底面积的一半，则此截面分圆锥的高为上、下两段
的比为（ A ）
A．1:(-1) B．1:2 C．1: D．1:4
10、下列命题中错误的是（ B ）.
A. 若
，则
B. 若
，
，则
C. 若
，，
，则
D. 若，
=AB，//，AB，则
11、直线
与圆
相切，则的值为（ C ）.
A. 1，
B. 
C.
D.
1
12、设入射光线沿直线 y=2x+1 射向直线 y=x, 则被y=x 反射后,反射光线所在的
直线方程是( )
A．x-2y-1=0 B．x-2y+1=0 C．3x-2y+1=0 D．x+2y+3=0
二、填空题（每小题4分，共4小题16分）
13、函数y=
的定义域是
｛xx
｝
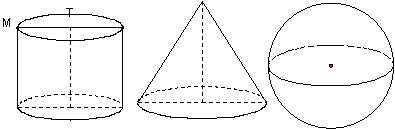
14、一个圆柱和一个圆锥的底面直径和他们的高都与某一个球的直径相等，这时
圆柱、圆锥、球的体积之比为 ．3:1:2
 |
15. 
0 ；若
4 .
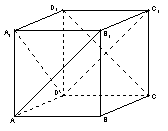16. 如图，在正方体
中，异面
直线
与
所成的角为_______度；直线
与平面
所成的角为_______度. 
，
三：解答题：
17：设全集U为R,已知A={x1<x<7},B={xx<3或x>5},
求（1）A
B (2)AB
(3)(CUA)(CUB)
解（1）R ; (2){x1<x<3或5<x<7}; (3){xx
}.
18. 求经过两条直线
：
与
：
的交点
，且垂直于直线
：
直线的方程.
解：由
解得
∴ 点P的坐标是（，2）
∵ 所求直线与垂直，
∴ 设直线的方程为 
把点P的坐标代入得 
，得
∴ 所求直线的方程为
19. 已知圆心为
的圆经过点
（0，
），
（1，
），且圆心在直线：
上，求圆心为的圆的标准方程.
解：因为（0，），（1，），所以线段
的中点
的坐标为
，
直线的斜率 
，
因此线段的垂直平分线
的方程是
，
即
圆心的坐标是方程组 
，的解.
解此方程组，得
，
所以圆心的坐标是（
，）.
圆心为的圆的半径长
所以，圆心为的圆的标准方程是
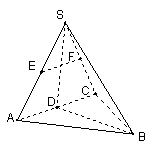
20. 如图：在三棱锥
中，已知点、
、
分别为棱
、
、
的中点.
①求证：
∥平面
.
②若
，
，求证：平面
⊥平面 .
解：①证明：∵是
的中位线，
∴∥，
又∵
平面，平面，
∴∥平面.
②证明：∵,
∴
，
∵,
∴
,
又∵
平面，
平面，
，
∴
平面，
又∵
平面，
∴平面⊥平面.
21、 光线通过一块玻璃,其强度要损失
,把几块这样的玻璃重叠起来,设光线原来的强度为,通过
块玻璃后强度为
.
（1）写出关于的函数关系式；
（2）通过多少块玻璃后，光线强度减弱到原来的
以下? ( 
解析:
(1) 
(2) 
∴ 
.
22 、已知函数
.
（1）求证：不论为何实数
总是为增函数；
（2）确定的值, 使为奇函数；
（3）当为奇函数时, 求的值域.
解析: (1) 
的定义域为R, 设
,
则
=
,
, 
,
即
,所以不论为何实数
总为增函数.
(2) 为奇函数,
,即
,
解得: 
（3）
由(2)知
, 
,
,
所以的值域为