高一上学期期末数学试卷
班级 姓名 学号 得分 .
一、填空题
1、“![]() 且
且![]() ”是“
”是“![]() ,且
,且![]() ”的 条件.
”的 条件.
2、“若![]() ,则
,则![]() ”是 (真或假)命题.
”是 (真或假)命题.
3、已知![]() ,
,![]() ,则
,则![]() .
.
4、已知![]() 是
是![]() 上的偶函数,且
上的偶函数,且![]() 在
在![]() 上是增函数,若
上是增函数,若![]() ,则
,则![]() 的取值范围是 .
的取值范围是 .
5、若关于![]() 的一元二次不等式
的一元二次不等式![]() 在实数范围内恒不成立,则实数
在实数范围内恒不成立,则实数![]() 的取值范围是__________.
的取值范围是__________.
6、![]() 在
在![]() 上的减函数,则
上的减函数,则![]() 的取值范围
.
的取值范围
.
7、函数![]() 的单调递减区间是 .
的单调递减区间是 .
8、若![]() ,
,![]() ,
,![]()
![]() ,下列4个命题:①
,下列4个命题:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,其中真命题的序号是 .
,其中真命题的序号是 .
9、若![]() ,则
,则![]() 的范围是 .
的范围是 .
10、已知定义域为![]() 的函数
的函数![]() ,
,![]() 且对任意
且对任意![]() ,
,
满足![]() ,试写出具有上述性质的一个函数
.
,试写出具有上述性质的一个函数
.
二、选择题
11、“![]() ”是“
”是“![]() ”的( )
”的( )
A、充分非必要条件 B、必要非充分条件
C、充要条件 D、既非充分又非必要条件
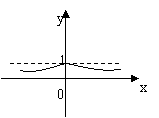
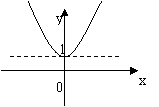 12、函数
12、函数![]() 的图像是( )
的图像是( )
A B
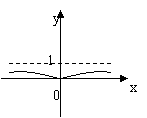 | |||
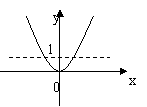 | |||
C D
13、若集合![]() ,
,![]() ,则
,则![]() =(
)
=(
)
A、![]() B、
B、![]()
C、![]() D、
D、![]()
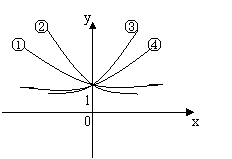 14、如图①
14、如图①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,根据图像可得
,根据图像可得![]() 、
、![]() 、
、![]() 、
、![]() 与1的大小关系为( )
与1的大小关系为( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
三、解答题
15、解不等式:![]() .
.
16、已知函数![]() ,判断函数
,判断函数![]() 的奇偶性,并说明理由.
的奇偶性,并说明理由.
17、作出函数![]()
![]() 的图像,并写出它的单调区间.
的图像,并写出它的单调区间.
 |
18、将长为12米的钢筋截成12段,做成底面为正方形的长方体水箱骨架,问水箱的高![]() 及底面边长
及底面边长![]() 分别为多少时,这个水箱的表面积为最大?并求出这个水箱最大的表面积.
分别为多少时,这个水箱的表面积为最大?并求出这个水箱最大的表面积.
 |
19、已知![]()
(1)求![]() 的定义域;
的定义域;
(2)判断![]() 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(3)当![]() 时,求使
时,求使![]() 的
的![]() 取值范围.
取值范围.
高一数学参考答案
一、填空题:
1、![]() 2、充分非必要 3、假 4、
2、充分非必要 3、假 4、![]()
![]()
5、![]() 6、
6、![]() 7、
7、![]() 8、
8、![]()
9、①③ 10、![]() 11、如
11、如![]() …
…
二、选择题:(11-14题)A、B、C、B
三、解答题
15、解:![]()
![]()
![]()
![]()
![]()
16、解:![]() ,又
,又![]()
![]()
![]() 为奇函数.
为奇函数.
17、解:图略,单调递增区间为![]()
![]() 与
与![]() ;单调递减区间为
;单调递减区间为 ![]() 与
与![]()
18、解:由题得![]()
水箱的表面积![]()
![]()
![]() =
=![]() =
=![]()
![]() 当
当![]() 时,
时,![]() 此时
此时![]() ,
,
![]() 当水箱的高
当水箱的高![]() 与底面边长
与底面边长![]() 都为1米时,这个水箱的表面积最大,最大值为6平方米
都为1米时,这个水箱的表面积最大,最大值为6平方米
19、解:
(1)![]() ,
,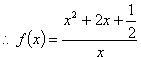
![]() =
=![]()
![]() +2
+2
当且仅当![]() 即
即![]() 时等号成立
时等号成立 ![]() .
.
(2)对任意![]() ,
, ![]() 恒成立
恒成立
等价于![]() 在
在![]() 上恒成立.
上恒成立.
又![]()
![]() 在
在![]() 单调递增,
单调递增,
![]() 只要
只要![]() ,
,![]() 即
即![]() .
.