高一下学期段考二数学试题
2008年5月31
第I卷
参考公式:
样本数据![]() 的标准差
的标准差 ![]()
一.选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的,并将答案填涂在答题卡上.
1.![]() =
( )
=
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2.![]() 为第几象限的角
( )
为第几象限的角
( )
A.第一象限或第三象限 B.第一象限
C.第一象限或第四象限 D.第二象限或第三象限
3.下列说法正确的是 ( )
A.向量![]() 的长度与向量
的长度与向量![]() 的长度相等,方向相反
的长度相等,方向相反
B.向量![]() 与
与![]() 平行,则
平行,则![]() 与
与![]() 的方向相同或相反
的方向相同或相反
C.向量![]() 与向量
与向量![]() 是共线向量,则A、B、C、D必在同一直线上
是共线向量,则A、B、C、D必在同一直线上
D.单位向量都相等
4.函数![]() 是
( )
是
( )
A.周期为![]() 的奇函数 B.周期为
的奇函数 B.周期为![]() 的偶函数 C.周期为
的偶函数 C.周期为![]() 的奇函数 D.周期为
的奇函数 D.周期为![]() 的偶函数
的偶函数
5.已知一组数据: ![]() 的平均数是
的平均数是![]() , 那么,这组数据的标准差是 ( )
, 那么,这组数据的标准差是 ( )
A.
4
B.2
C. ![]() D.
10
D.
10
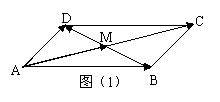 6.如图(1),在平行四边形
6.如图(1),在平行四边形![]() 中,点
中,点![]() 是对角线的交点,关于下列说法,正确的个数的是 ( )
是对角线的交点,关于下列说法,正确的个数的是 ( )
①![]() ②
②![]() ③
③![]()
④向量![]() ,
,![]() 不能作为这一平面的一组基底
不能作为这一平面的一组基底
 A.1个
B.2个 C.3个 D.4个
A.1个
B.2个 C.3个 D.4个
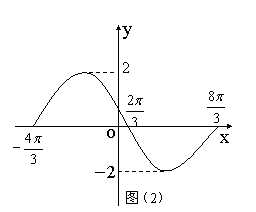
7.函数![]() 在一个周期上的图象为图(2)所示.
在一个周期上的图象为图(2)所示.
则函数的解析式是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
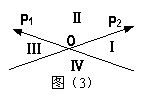 8.如图(3),平面内的两条相交直线
8.如图(3),平面内的两条相交直线![]() 将平面分成四个部分Ⅰ、
将平面分成四个部分Ⅰ、
Ⅱ、Ⅲ、Ⅳ(不包括边界),若![]() ,且点
,且点![]() 落在第Ⅲ
落在第Ⅲ
部分,则实数![]() 满足
( )
满足
( )
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
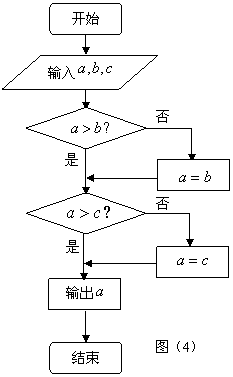
9.如图(4)所示的算法中,令![]() ,
,
若在集合![]() 中,
中,
给![]() 取定一个值,输出的结果是
取定一个值,输出的结果是![]() ,则
,则![]() 所在的范围是( )
所在的范围是( )
A.
![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
10.设![]() 为三个非零向量,若
为三个非零向量,若![]() ,则
,则![]() 的取
的取
值范围是( )
A.
![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
二.填空题:本大题共4小题,每小题5分,满分20分.
11.某中学有高一、高二、高三学生共1 600名,其中高三学生400名.如果用分层抽样的方法从这1 600人抽取一个160人的样本,那么应当从高三学生中抽取的人数是_________________.
12.已知![]() ,
,![]() ,则向量
,则向量![]() 与
与![]() 的夹角为______________,
的夹角为______________,![]() ______________.
______________.
13. 某科研小组共有5个成员,其中男研究人员3人,女研究人员2名,现选举2名代表,那么
至少有1名女研究人员当选的概率为___________________.
14.给出下列命题:
①函数![]() 的图象向左平移
的图象向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象.
的图象.
②若![]() 、
、![]() 是第一象限的角且
是第一象限的角且![]()
③若![]() 是锐角
是锐角![]() 的任意两个内角,则一定有
的任意两个内角,则一定有![]() 成立
成立
④![]() 是函数
是函数![]() 的一条对称轴方程
的一条对称轴方程
⑤已知函数![]() ,若
,若![]() ,则
,则![]() 必是
必是![]() 的整数倍
的整数倍
其中正确命题的序号是____________________.(写出所有正确命题的序号)
第II卷
二.填空题(每题5分,共20分)
11. 12.
13. 14.
三.解答题(共6个小题,共80分;解答应写出文字说明,证明过程或演算步骤)
15.(本题12分) 已知角![]() 的顶点与直角坐标系的原点重合,始边在
的顶点与直角坐标系的原点重合,始边在![]() 轴的非负半轴上,终边经过点
轴的非负半轴上,终边经过点![]() ,求
,求![]() 的值.
的值.
16. (本题13分)已知向量![]() ,分别求使下列结论成立的实数
,分别求使下列结论成立的实数![]() 的值
的值
(Ⅰ)![]() ;
;
(Ⅱ)![]() ;
;
17. (本题13分)已知点![]() .
.
(Ⅰ)若![]() ,求
,求![]() 和
和![]() 的值
的值
(Ⅱ)若![]() ,其中
,其中![]() 为坐标原点,求
为坐标原点,求![]() 的值.
的值.
18. (本题14分)设函数![]() 的图象关于点
的图象关于点![]() 对称.
对称.
(Ⅰ)求![]() ;
;
(Ⅱ)求函数![]() 的单调增区间;
的单调增区间;
(Ⅲ)求函数![]() 在
在![]() 上的最大值和取最大值时的
上的最大值和取最大值时的![]() .
.
19. (本题14分)如图(5)所示,已知![]() 设
设![]() 是直线
是直线![]() 上的一点, (其中
上的一点, (其中![]() 为坐标原点).
为坐标原点).
(Ⅰ)求使![]() 取最小值时的点
取最小值时的点![]() 的坐标和此时
的坐标和此时![]() 的余弦值.
的余弦值.
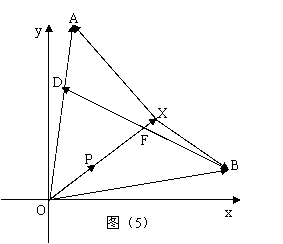 (Ⅱ)对于(Ⅰ)中的
(Ⅱ)对于(Ⅰ)中的![]() .若
.若![]() 是线段
是线段![]() 的三等分点,且
的三等分点,且![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,设
,设![]()
![]() 试用
试用![]() 表示
表示![]() 和
和![]() .
.
20. (本题14分)设![]() ,函数
,函数![]() 的定义域为
的定义域为![]() ,且
,且![]() ,当
,当![]() ,有
,有
![]() ;函数
;函数![]() 是定义在
是定义在![]() 上单调递增的奇函数.
上单调递增的奇函数.
(Ⅰ)求![]() 和
和![]() 的值(用
的值(用![]() 表示);
表示);
(Ⅱ)求![]() 的值;
的值;
(Ⅲ)当![]() 时,
时, ![]() 对所有的
对所有的![]() 均成立,求实数
均成立,求实数![]() 的取值范围.
的取值范围.
四.附加题 (本题满分10分,该题得分加入总分中,全卷总分上限为150分)
21.设![]() 是定义在
是定义在![]() 上以2为周期的函数,对
上以2为周期的函数,对![]() ,用
,用![]() 表示区间
表示区间![]() .
.
已知当![]() 时,函数
时,函数![]() .
.
(1)
求![]() 在
在![]() 上的解析式;
上的解析式;
(2)
对自然数![]() ,求集合
,求集合![]() {
{![]() 使方程
使方程![]() 在
在![]() 上有两个不相等的实根}.
上有两个不相等的实根}.
高一下学期段考2数学试题
答案及评分标准
一.选择题:本大题共10小题;每小题5分,共50分.
1.B 2.A 3.A 4.D 5.C 6.C 7.A 8.B 9.D 10.C
二.填空题:本大题共4小题,每小题5分,满分20分.
11.
______40_________.
12.____![]() ______ _____
______ _____![]() _____.
_____.
13.
_______![]() _______.
14.____③④______.
_______.
14.____③④______.
三.解答题:本大题共6个小题,满分80分;解答应写出文字说明、证明过程或演算步骤.
15.(本题12分)
已知角![]() 的顶点与直角坐标系的原点重合,始边在
的顶点与直角坐标系的原点重合,始边在![]() 轴的非负半轴上,终边经过点
轴的非负半轴上,终边经过点![]() ,求
,求![]() 的值.
的值.
解:由三角函数的定义可知,
![]() ------------3分
------------3分
![]() ------------5分
------------5分
![]() ---------------7分
---------------7分
因为![]() ---------10分(每个公式1分)
---------10分(每个公式1分)
![]() -------------12分
-------------12分
16.(本题12分)
已知向量![]() ,分别求使下列结论成立的实数
,分别求使下列结论成立的实数![]() 的值
的值
(Ⅰ)![]() ;
;
(Ⅱ)![]() .
.
解(Ⅰ)因为![]() ,所以
,所以![]() --------2分
--------2分
![]() --------------5分(只要用了垂直的公式就可以酌情给分)
--------------5分(只要用了垂直的公式就可以酌情给分)
![]() -----------6分
-----------6分
(Ⅱ)因为![]() ,所以
,所以![]() ---------8分
---------8分
![]() ------------------------11分(只要用了共线的公式就可以酌情给分)
------------------------11分(只要用了共线的公式就可以酌情给分)
![]() -----------12分
-----------12分
17. (本题14分)
已知点![]() .
.
(Ⅰ)若![]() ,求
,求![]() 和
和![]() 的值;
的值;
(Ⅱ)若![]() ,其中
,其中![]() 为坐标原点,求
为坐标原点,求![]() 的值.
的值.
解:(Ⅰ)![]()
![]() ------------1分
------------1分
![]() -------2分
-------2分
![]() --------3分
--------3分
![]() --------4分
--------4分
因为![]() -------------5分
-------------5分
![]() ----------7分
----------7分
![]() ------------------8分
------------------8分
(Ⅱ)![]() -----------------------9分(只要写出
-----------------------9分(只要写出![]() 就给分)
就给分)
![]() ---------------10分
---------------10分
![]() -----------12分
-----------12分
![]() ----------13分
----------13分
![]() ----------14分
----------14分
18.(本题14分)
设函数![]()
![]() 的图象关于点
的图象关于点![]() 对称.
对称.
(Ⅰ)求![]() ;
;
(Ⅱ)求函数![]() 的单调增区间;
的单调增区间;
(Ⅲ)求函数![]() 在
在![]() 上的最大值和取最大值时的
上的最大值和取最大值时的![]() .
.
解: (Ⅰ)因为函数![]() 的图象关于点
的图象关于点![]() 对称,所以图象经过点
对称,所以图象经过点![]() ----------------1分
----------------1分
![]()
![]() ----------------3分
----------------3分
因为![]() ,所以
,所以![]() ---------------4分
---------------4分
(Ⅱ)函数为![]() ,
,
因为![]() 在
在![]() 内单调增,-----------5分
内单调增,-----------5分
所以当![]()
![]()
![]() ---------8分
---------8分
所以![]() 的单调增区间为
的单调增区间为![]() ----9分(未说明
----9分(未说明![]() 或没有用区间和集合的扣1分)
或没有用区间和集合的扣1分)
(Ⅲ)因为![]() --------10分
--------10分
令![]() ,
,
由![]() 的图象和单调性可知
的图象和单调性可知![]() --------12分
--------12分
![]() ,且当
,且当![]() 时,--------------13分
时,--------------13分
函数取得最大值为2.-----------14分
19. (本题14分)
如图(5)所示,已知![]() 设
设![]() 是直线
是直线![]() 上的一点,(其中
上的一点,(其中![]() 为坐标原点).
为坐标原点).
(Ⅰ)求使![]() 取最小值时的点
取最小值时的点![]() 的坐标和此时
的坐标和此时![]() 的余弦值.
的余弦值.
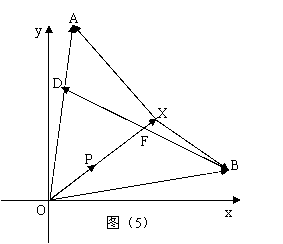 (Ⅱ)对于(Ⅰ)中的
(Ⅱ)对于(Ⅰ)中的![]() .若
.若![]() 是线段
是线段![]() 的三等分点,且
的三等分点,且![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,设
,设![]()
![]() 试用
试用![]() 表示
表示![]() 和
和![]() .
.
解: (Ⅰ)因为![]() 三点共线,所以
三点共线,所以![]() -----1分
-----1分
![]() --------2分
--------2分
![]() --------4分
--------4分
所以当![]() 即
即![]() 时,
时, ![]() 取最小值--------5分
取最小值--------5分
此时![]()
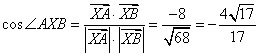 ----------7分
----------7分
(Ⅱ) 因为![]() ,令存在实数
,令存在实数![]() ,使得
,使得![]()
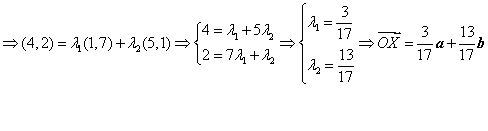 ------9分
------9分
因为![]() ,由B,F,D三点共线,可知存在实数
,由B,F,D三点共线,可知存在实数![]() 使得
使得![]()
![]()
![]()
------11分
又因为O,F,X三点共线,所以存在实数![]() 使得,
使得,
![]() ---------------13分
---------------13分
所以
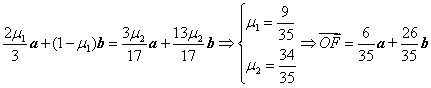 ---------14分
---------14分
20. (本题14分)
设![]() ,函数
,函数![]() 的定义域为
的定义域为![]() ,且
,且![]() ,当
,当![]() ,有
,有
![]() ;函数
;函数![]() 是定义在
是定义在![]() 上单调递增的奇函数
上单调递增的奇函数
(Ⅰ)求![]() 和
和![]() 的值(用
的值(用![]() 表示)
表示)
(Ⅱ)求![]() 的值
的值
(Ⅲ)当![]() 时,
时, ![]() 对所有的
对所有的![]() 均成立,求实数
均成立,求实数![]() 的取值范围
的取值范围
解(Ⅰ) 因为当![]() ,有
,有![]()
所以,令![]() ------------------2分
------------------2分
所以,令![]() ------------------4分
------------------4分
(Ⅱ) 令![]()
![]()
令![]()
![]() ----------------6分
----------------6分
所以![]() 或
或![]() 或
或![]()
![]() ------------8分
------------8分
(Ⅲ) 因为![]() 是定义在
是定义在![]() 上单调递增的奇函数,所以
上单调递增的奇函数,所以![]()
![]() -----------9分
-----------9分
令![]() ----------10分
----------10分
原题等价于“对于任意![]() ,
,![]() 恒成立” ----------10分
恒成立” ----------10分
令函数![]()
所以对称轴![]()
①当![]() 时,只需满足
时,只需满足![]() (舍去)----------11分
(舍去)----------11分
②当![]() 时,只需满足----------12分
时,只需满足----------12分
![]() ,以
,以![]()
③当![]() 时,只需满足
时,只需满足![]() 所以
所以![]() -----13分
-----13分
综上所述:![]() --------------14分
--------------14分
(本题(Ⅲ)还可以用分离变量法或数形结合,其它方法酌情给分)
四.附加题 (本题满分10分,该题得分加入总分中,全卷总分上限为150分)
21.设![]() 是定义在
是定义在![]() 上以2为周期的函数,对
上以2为周期的函数,对![]() ,用
,用![]() 表示区间
表示区间![]() .
.
已知当![]() 时,函数
时,函数![]() .
.
(1)
求![]() 在
在![]() 上的解析式;
上的解析式;
(2)
对自然数![]() ,求集合
,求集合![]() {
{![]() 使方程
使方程![]() 在
在![]() 上有两个不相等的实根}.
上有两个不相等的实根}.
解:(1)因为![]() 是以2为周期的函数,所以当
是以2为周期的函数,所以当![]() 时,
时,![]() 是
是![]() 的周期函数
的周期函数
又当![]() 时,
时,![]() ,所以
,所以![]() ,
,
 即当
即当![]() ,
,![]() 时,
时,![]() .
…………………………..3分;
.
…………………………..3分;
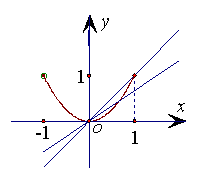
(2)[1] 当![]() 时,
时, ![]() 表示区间
表示区间![]() , 此时
, 此时![]() , 令
, 令![]() 则欲使方程
则欲使方程![]() 有两个不等根,即使
有两个不等根,即使![]() 与
与![]() 这两个函数图像有两个不同交点.如图所示,
这两个函数图像有两个不同交点.如图所示,
只要:![]()
![]() 或
或![]()
![]() 即可………5分
即可………5分
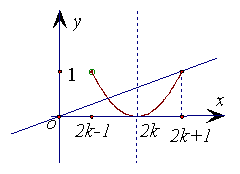 [2] 当
[2] 当![]() 时,
时, ![]() 表示区间
表示区间![]() , 此时
, 此时![]() , 令
, 令![]() 则欲使方程
则欲使方程![]() 有两个不等根,即使
有两个不等根,即使![]() 与
与![]() 这两个函数图像有两个不同交点.如图所示,
这两个函数图像有两个不同交点.如图所示,
只要:![]()
![]()
![]() 即可……….7分
即可……….7分
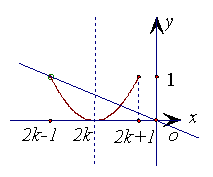 [3] 当
[3] 当![]() 时,
时, ![]() 表示区间
表示区间![]() , 此时
, 此时![]() , 令
, 令![]() 则欲使方程
则欲使方程![]() 有两个不等根,即使
有两个不等根,即使![]() 与
与![]() 这两个函数图像有两个不同交点.如图所示,
这两个函数图像有两个不同交点.如图所示,
只要:![]()
![]()
![]() 即可……………9分
即可……………9分
综上所述:[1] 当![]() 时,
时, ![]()
![]() 或
或![]()
![]() ;
;
[2] 当![]() 时,
时, ![]()
![]()
![]() ;
;
[3] 当![]() 时,
时, ![]()
![]()
![]() ……………….10分
……………….10分
注: 本题还可以用“根的分布”的方法,请酌情给分.