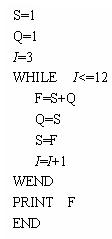_____班；姓名______
学号__________ 高一第二学期·必修三之统计单元测试
撰稿： 方锦昌 电子邮箱 fangjingchang2 或@.com 手机号码
一:选择题:
1．
名工人某天生产同一零件，生产的件数是
设其平均数为
,
中位数为
,众数为
，则有( )
A． 
B．
C．
D．
2．某同学使用计算器求
个数据的平均数时，错将其中一个数据
输入为
，那么由此求出的
平均数与实际平均数的差是( ) A．
B．
C．
D．
3．要从已编号（
）的
枚最新研制的某型导弹中随机抽取
枚来进行发射试验，用每部分
选取的号码间隔一样的系统抽样方法确定所选取的枚导弹的编号可能是（ ）
A．
B．
C．
D．
4．容量为
的样本数据，按从小到大的顺序分为
组，如下表：
| 组号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 频数 | 10 | 13 | x | 14 | 15 | 13 | 12 | 9 |
第三组的频数和频率分别是 ( )
A．
和
B．和 C． 
和 D． 
和
5．一个容量为
的样本数据分组后组数与频数如下：［25，25.3），6；［25.3，25.6），4；［25.6，
25.9），10；［25.9，26.2），8；［26.2，26.5），8；［26.5，26.8），4；则样本在［25，25.9）上的频
率为（ ）A．
B．
C．
D．
6．某公司有员工49人，其中30岁以上的员工有14人，没超过30岁的员工有35人，为了解员
工的健康情况，用分层抽样的方法抽一个容量为7的样本，其中30岁以上的员工应抽多少( )
A．2人 B．4人 C．5人 D．1人
7．把21化为二进制数，则此数为( )
A．10011(2) B．10110(2) C．10101(2) D．11001(2)
8. 在抽取产品的尺寸过程中，将其尺寸分成若干组，
是其中一组，抽查出的个体在该组
上的频率为m ，该组上的直方图的高为h，则
(
)
A．hm B．
C．
D．h+m
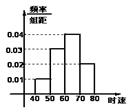
9、现有
辆汽车通过某一段公路时的时速的频率分布直方图如右图所示，
时速在
的汽车大约有（ ）
.辆
.辆 
.辆
.80辆
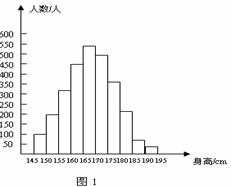10．(2007年广东高考题)图1是某县参加2007年高考的学生身高条形统计图，从左到右的各
条形表示的学生人数依次记为
（如
表示身高（单位：cm）在
内的学生人数）．
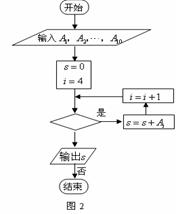
图2是统计图1中身高在一定范围内学生人数的一个算法流程图．现要统计身高在160～180cm（含160cm，不含180cm）的学生人数，那么在流程图中的判断框内应填写的条件是（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
二:填空题
11．经问卷调查，某班学生对摄影分别执“喜欢”、“不喜欢”和“一般”三种态度，其中执“一般”
态度的比“不喜欢”态度的多
人，按分层抽样方法从全班选出部分学生座谈摄影，如果选出的
位“喜欢”摄影的同学、
位“不喜欢”摄影的同学和位执“一般”态度的同学，那么全班学
生中“喜欢”摄影的比全班人数的一半还多 人。
12．数据
的标准差是______________。
13．数据
的方差为
，平均数为
，则
（1）数据
的标准差为 ，平均数为 ．
（2）数据
的标准差为 ，平均数为 。
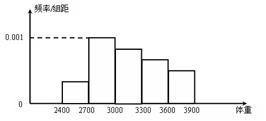
14．观察新生婴儿的体重，其频率分布直方图如图所示，则新生婴儿体重在
的频率为 。
15．已知样本
的平均数是，标准差是
，则
.
| 组距 |
|
|
|
|
|
|
| 频数 | 2 | 3 | 4 | 5 | 4 | 2 |
16． 一个容量为
的样本数据，分组后组距与频数如右表所示：则样本在区间
上的频率为_________________。
17．某单位有老年人
人，中年人
人，青年人
人，为调查身体健康状况，需要从中抽取一个
容量为
的样本，用分层抽样方法应分别从老年人、中年人、青年人中各抽取 人、 人、______人。
三:解答题
18．为了了解初三学生女生身高情况，某中学对初三女生身高进行了一次测量，所得数据整理
后列出了频率分布表如下：
| 组 别 | 频数 | 频率 |
| 145.5～149.5 | 1 | 0.02 |
| 149.5～153.5 | 4 | 0.08 |
| 153.5～157.5 | 20 | 0.40 |
| 157.5～161.5 | 15 | 0.30 |
| 161.5～165.5 | 8 | 0.16 |
| 165.5～169.5 | M | n |
| 合 计 | M | N |
（1）求出表中
所表示的数分别是多少？（2）画出频率分布直方图.
（3）全体女生中身高在哪组范围内的人数最多？
19． 某校高中部有三个年级，其中高三有学生
人，现采用分层抽样法抽取一个容量为
的
样本，已知在高一年级抽取了
人，高二年级抽取了人，则高中部共有多少学生？
20．以下是某地搜集到的新房屋的销售价格
和房屋的面积
的数据：
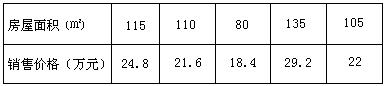
（1）画出数据对应的散点图；
（2）求线性回归方程，并在散点图中加上回归直线；
（3）据（2）的结果估计当房屋面积为
时的销售价格.
21．已知
、
且
，
．
求
的值．
22(2007年广东高考题)．下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产
量x（吨）与相应的生产能耗y（吨标准煤）的几组对照数据
| ｘ | ３ | ４ | ５ | ６ |
| ｙ | ２．５ | ３ | ４ | ４．５ |
（１） 请画出上表数据的散点图；
（２）
请根据上表提供的数据，用最小二乘法求出ｙ关于ｘ的线性回归方程
；
（３） 已知该厂技术改造前１００吨甲产品能耗为９０吨标准煤；试根据（２）求出的线性
回归方程，预测生产１００吨甲产品的生产能耗比技术改造前降低多少吨标准煤？
（3×2．5+4×3+5×4+6×4.5=66.5）
23题. 意大利数学家菲波拉契,在1202年出版的一书里提出了这样的一个问题:一对兔子饲养到
第二个月进入成年,第三个月生一对小兔,以后每个月生一对小兔,所生小兔能全部存活并且也是
第二个月成年,第三个月生一对小兔,以后每月生一对小兔.问这样下去到年底应有多少对兔子?
试画出解决此问题的程序框图,并编写相应的程序.
参考答案:
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | B | B | A | C | A | C | B | C | B |
11题、；因为位执“一般”对应位“不喜欢”，即“一般”是“不喜欢”的倍，而他们的差
为人，即“一般”有
人，“不喜欢”的有人，且“喜欢”是“不喜欢”的倍，即人，
全班有人，
12． 
因为 
13题．解:（1）
，
（2），
14题．0．3； 15题．96； 16题．0.7； 17题．6人；12人；18人
18题．解：（1）
（3）在
范围内最多
19题． 解：从高三年级抽取的学生人数为
而抽取的比例为
，高中部共有的学生为
20题．解：（1）数据对应的散点图如图所示：
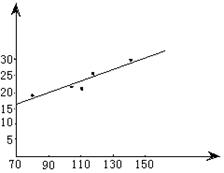
（2）
，
，
设所求回归直线方程为
，则
;
故所求回归直线方程为
（3）据（2），当
时，销售价格的估计值为：
（万元）
21．解：∵
∴
∴
）
∴
∴
又∵ ∴ 
∴
∴
∴
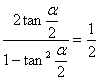
22题．解 方法1（不作要求）：设线性回归方程为
，则
∴
时， 
取得最小值
即
，∴
时ｆ（ａ，ｂ）取得最小值；
所以线性回归方程为
；
方法2：由系数公式可知，
，所以线性回归方程为；
（４）
ｘ＝１００时，
，所以预测生产１００吨甲产品的生产能耗比技术
改造前降低１９．６５吨标准煤．
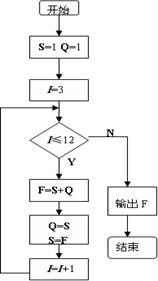
23题.解: 分析: 根据题意可知,第一个月有1对小兔,第二个月有1对成年兔子,第三个月有两对兔子,
从第三个月开始,每个月的兔子对数是前面两个月兔子对数的和,设第N个月有两F对兔子,第N－1个
月有S对兔子,第N－2个月有Q对兔子,则有F=S+Q,一个月后,即第N+1个月时,式中变量S的新值应
变第N个月兔子的对数(F的旧值),变量Q的新值应变为第N－1个月兔子的对数(S的旧值),这样,用
S+Q求出变量F的新值就是N+1个月兔子的数,依此类推,可以得到一个数序列,数序列的第12项就
是年底应有兔子对数,我们可以先确定前两个月的兔子对数均为1,以此为基准,构造一个循环程序,
让表示“第×个月的I从3逐次增加1,一直变化到12,最后一次循环得到的F”就是所求结果.
流程图和程序如下:
