高一第一学期数学月考测验试卷 姓名_______
测验内容:P1—61面(集合、函数、指数及指数函数) 学号________
班级_________
撰稿: 方锦昌 电子邮箱 fangjingchang2 手机号码
一、选择题:(5×10=50′)
★1、己知全集I={1,2,3,4,5}, M ={1,2}, N={1,3,5},则M∩CIN等于:
A、{1,2} B、{2,3} C、{2} D、{2,4}
★2、下列函数中既不是奇函数又不是偶函数的是:
A、f(x)=1-x B、f(x)=x-x3 C、f(x)=![]() D、f(x)=x
D、f(x)=x
★3、函数y=ax-1+2(a>0,a≠1)一定经过的定点是:
A、(0,1) B、(1,1) C、 (1,2) D、 (1,3)
★4、函数f(x)=![]() +(x-4)0的定义域为:
+(x-4)0的定义域为:
A. {xx>2,x≠4} B、{xx≥2,或x≠4} C、![]() D、
D、![]()
 ★5、函数y=x2-1的值域是:
★5、函数y=x2-1的值域是:
A. (-∞,-1) B、 ![]() C、 [-1,0]
D、 R
C、 [-1,0]
D、 R
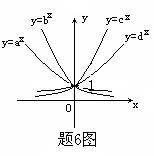
★6、指数函数y=ax,y=bx,y=cx,y=dx的图像如图所示,则a、b、c、d以及1之间的大小关系是:
A、a<b<1<c<d B、a<b<1<d<c
C、 b<a<1<d<c D、c<d<1<a<b
★7、设偶函数f(x)的定义域为R,当x![]() 时f(x)是增函数,则f(-2),f(
时f(x)是增函数,则f(-2),f(![]() ),f(-3)的大小关系是:
),f(-3)的大小关系是:
A、f(![]() )>f(-3)>f(-2) B、f(
)>f(-3)>f(-2) B、f(![]() )>f(-2)>f(-3)
)>f(-2)>f(-3)
C、f(![]() )<f(-3)<f(-2) D、f(
)<f(-3)<f(-2) D、f(![]() )<f(-2)<f(-3)
)<f(-2)<f(-3)
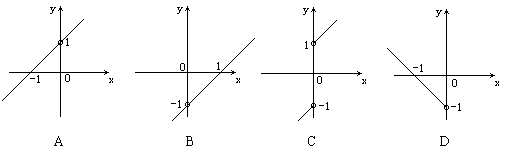 ★8、函数
★8、函数![]() 的图象是:
的图象是:
★9、函数y=x2+4x+5(其中x∈[-3,1)的值域为:
A [2,10) B、[1,10) C、[2,10] D、[1,10]
★10、已知函数![]() 为R上的减函数,则满足
为R上的减函数,则满足![]() 的实数
的实数![]() 的取值范围是:
的取值范围是:
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
●选择题答案
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答 案 |
二、 填空题(5×5=25′)
★11、集合{0,1}的所有真子集是_____________________________.
★12、设函数![]() 为奇函数,则实数
为奇函数,则实数![]() ______________。
______________。
★13、已知函数y=x2-2ax-3在(2,+∞)上是增函数,则a的取值范围是___________.
 ★14、已知集合
★14、已知集合![]() ,
,![]() ,若A∩B=Æ,则实数
,若A∩B=Æ,则实数![]() 的取值范围是:_____________________________________.
的取值范围是:_____________________________________.
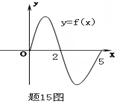
★15、设奇函数f(x)的定义域为[−5,5].若当x∈[0,5]时,f(x)的图象 如右图,则不等式f(x)<0的解集是 .
三、 解答题(12+12+12+13+13+13=75′)
★16题(12分)、①、已知f(x)=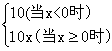 求f[f(-7)]之值。
求f[f(-7)]之值。
(2)、已知f(x)=3x2+1,g(x)=2x-1,求f[g(x)].
★ 17题(12分)、给定集合A、B,定义一种新运算: A*B={ x x∈A或x∈B,
但xÏA∩B },又已知A={0,1,2,},B={1,2,3},用列举法写出A*B.
★18题(12分)、已知集合![]() ,集合
,集合![]() 。
。
(1)、若![]() ,求a的范围;
,求a的范围;
(2)、若全集U=R且![]() ,求a的范围。
,求a的范围。
 |
★19题(13分)、对于函数f(x)=x2-2x,
(1)、判断其奇偶性,并指出图象的对称性;
(2)、画此函数的图象,并指出其单调区间。
★20题(13分):有一个小型自来水厂,蓄水池中有水450吨,水厂每小时可向蓄水池注水80吨,同时蓄水池又向居民小区供水,x小时内供水总量为80吨。现在开始向池中注水并同时向居民小区供水,问:
(1)、多少小时后蓄水池中的水量最少?
(2)、如果蓄水池中存水量少于150吨时,就会出现供水紧张,那么有几小时供水紧张?
★21题(13分):已知奇函数f(x)的定义域为(-∞,0)∪(0,+∞),且f(x)在(0,+∞)上为增函数,又f(1)=0,函数g(x)= -x2+mx+1-2m,x∈[0,1]
①、证明函数f(x)在(-∞,0)上也为增函数;
②、解关于x的不等式f(x)<0;
③、当x∈[0,1]时,求使得g(x)<0且f[g(x)]<0恒成立的m的取值范围。
参考答案
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | A | D | C | B | C | A | C | B | D |
第11题:Æ、{0}、{1};
第12题: -1; 第13题: {aa≤2} ; 第14题:{a2≤a≤3} ; 第15题: ![]()
★16(12分)、
(1)、∵f(-7)=10,∴f[f(-7)]=f(10)=100.
(2)、由已知得f[g(x)]=3(2x-1)2+1=12x2-12x+4
★17(12分)、
解:{0,3}
★18(12分)、
解:(1)a≤-4; (2)a>-2
★19题(13分)、
解.(1)偶函数;
(2)增区间:![]() ;
;
减区间:![]()
★20题(13分):
解:设x小时后蓄水池中的水量为y吨,则有y=(450+80x)-80
① 、y=80x-160+450=16(-5)2+50(x≥0)则当=5,即x=5时y有最小值,因此,在5小时后蓄水池中的水量最少。
② 、y=80x-160+450<150,则有<x<,即<x<,因为-=10,则有10小时供水紧张。
★21题(13分):
解:②、{xx<-1或0<x<1};③、m>4-2